R Final-term
결측값 X
read.table
1 | setwd("/Users/zerohertz") |
Data 취사 선택
indexing - []
1 | name[which(조건식),c('name1','name2',...)] |
1 | > Cars93[which(MPG.city>30),c('Model','Origin')] |
subset(select=, subset=)
1 | subset(name,select=c(name1,name2,...),subset=(조건식)) |
1 | > subset(Cars93,select=Model,subset=(MPG.city>30)) |
이산형 분포
| 분포 | ?의 횟수 | 베르누이 시행 | 기호(X~) | X | p(X=x) | R |
|---|---|---|---|---|---|---|
| 베르누이 | 성공 | O | Be(p) | 1번의 베르누이 시행 성공횟수 | $\displaystyle{p^x\times(1-p)^{1-x}}$ | binom() |
| 이항 | 성공 | O | B(n,p) | n번의 베르누이 시행 성공횟수 | ${}_n \mathrm{C}_x\times p^x\times(1-p)^{n-x}$ | binom() |
| 기하 | 시행 | O | G(p) | 처음 성공까지의 시행횟수 | $\displaystyle{q^{x-1}\times p}$ | geom() |
| 음이항 | 시행 | O | NB(k,p) | k번 성공까지의 시행횟수 | $(x-1)C(k-1) \times p^{k-1} \times (1-p)^{x-k}\times p$ | nbinom() |
| 포아송 | 성공 | O | $\displaystyle{P_0(\lambda)}$ | 단위(시간, 면적, …) 성공횟수 | $\displaystyle{e^{-\lambda} \times \lambda^x\over x!}$ | pois() |
| 초기하 | 성공 | X | HG(N,n,D) | 성공횟수 | ${}_DC_x \times (N-D)C(n-x) \over {}_N C_n$ | hyper() |
이항분포
- E(X)=np - 평균(성공횟수)
- V(X)=npq
기하분포
- 무한하게 시행시 무조건 성공(
p/(1-q)=1by 무한등비급수) - E(X)=1/p - 평균(시행횟수)
- V(X)=q/(p^2)
음이항분포
- 이항분포의 반대(
시행횟수<->성공횟수) - E(X)=k/p - 평균(시행횟수)
- V(X)=k*q/(p^2)
포아송분포
n->inf,p->0근사ex) p=0.001, n=3000- p(X=5)=3000C5((0.001)^5)*(0.999)^2995
- p(X=x)=(e^(-lambda)*lambda^x)/(x!)
- lambda=np
- p=(lambda)/n
- 이항분포에 근사하여 대입 후 증명
lambda- 평균성공횟수- E(X)=lambda
초기하분포
- 독립시행 X - 베르누이 시행을 따르지 않음
- 단순 확률 구하기와 Similar
- 변수
- N - 전체집단 개수
- n - 추출대상 개수
- D - 성공집단 개수
R
표
| mean | R |
|---|---|
| 이항분포 | binom() |
| 기하분포 | geom() |
| 음이항분포 | nbinom() |
| 포아송분포 | pois() |
| 초기하분포 | hyper() |
| 표본추출 - 이항 | rbinom(표본수,평균,분산) |
p(X=n) - 이항 |
dbinom(성공횟수,시행횟수,성공확률) |
p(X<=n) - 이항 |
pbinom(성공횟수,시행횟수,성공확률) |
p(X=n) - 기하 |
dgeom(실패횟수,성공확률) |
p(X=n) - 음이항 |
dnbinom(실패횟수,성공횟수,성공확률) |
p(X=n) - 포아송 |
dpois(성공횟수,lambda) |
p(X<=n)- 포아송 |
ppois(성공횟수,lambda) |
p(X=n)- 초기하 |
dhyper(성공횟수(x),성공표본수(D),다른표본수(N-D),추출개수(n)) |
| t 분포 | t() |
| F 분포 | f() |
| 정규분포 | norm() |
| 정규분포 함숫값 | dnorm() |
| 정규분포 누적 | pnorm() |
| 정규분포 x,z값(분위수) | qnorm(누적확률값) |
| 지수분포 | exp() |
r- 추출d- 확률p- 누적 확률q- 분위수
R source
1 | > ### 이산형 ### |
범주자료
1 | > summary(Cars93$AirBags) |
- 빈도
수치자료
1 | > summary(Length) |
- 평균
- 표준편차
- 중위수
수치자료 범주화
1 | > grade=ifelse(airquality$Temp>=60,'상','하');grade |
교차분석
범주자료 2개 - 두 범주형 자료간에 상호 관련성
검정통계량
$$\chi^2=\sum_{i}\sum_{j}\frac{(O_{ij}-E_{ij})^2}{E_{ij}} \sim \chi^2_{(a-1)(b-1)}$$
- a, b - 범주수
가설
$$H_0 : 두\ 변수\ 독립$$
기대빈도
독립이게끔 하는 빈도, 차이가 없게끔 하는 빈도 - $E_{ij}$
Example 1
$$H_0 : Origin과\ AirBags는\ 독립이다.$$
1 | > table(Origin,AirBags) |
- $p=0.786 \geq 0.05$이므로 $H_0$ 채택 - 독립
Example 2
$$H_0 : Origin과\ Type은\ 독립이다.$$
1 | > CrossTable(Origin,Type,expected=T,chisq=T) |
- $p=0.01511 \leq 0.05$이므로 $H_0$ 기각 - 독립 X
Large항목의 경우 기대빈도와 5~6 정도 차이가 나는 것을 볼 수 있음- $\frac{Column\ Total\ N \times Row\ Total\ N}{Total\ N} = Expected\ N$
- $\frac{(N-Expected\ N)^2}{Expected\ N} = Chi-square\ contribution$
- 검정통계량 : $\chi^2=14.08$
상관분석
수치자료 2개
검정통계량
$$T=r\sqrt{\frac{n-2}{1-r^2}}\sim t(n-2)$$
가설
$$H_0 : \rho_{xy}=0$$
상관계수
$$r_{xy}=\frac{\sum(x_i-\bar x)(y_i-\bar y)}{\sqrt{\sum(x_i-\bar x)^2\sum(y_i-\bar y)^2}}$$
Example
$$H_0 : \rho_{xy}=0$$
1 | > plot(Weight,EngineSize) |
- $p=0 \leq 0.05$이므로 $H_0$ 기각 - $\rho_{xy}\neq0$
일표본 T-검정
수치자료 1개
검정통계량
$$T=\frac{\bar{X}-\mu_0}{s/\sqrt{n}}\sim t(n-1)$$
가설
$$H_0:\mu=\mu_0$$
t.test()- 문제에 맞게 양측 단측
Example
1 | > mean(Price) |
- $\mu=19$ - 귀무가설 채택($0.6121\geq 0.05$)
- $\mu=25$ - 귀무가설 기각($3.667\times 10^-{7}\leq 0.05$)
독립표본 T-검정
집단 2개, 수치자료 1개 - 두 집단 평균비교
검정통계량
$$\sigma_1^2=\sigma_2^2\ -\ T=\frac{(\bar X_1 - \bar X_2)-(\mu_1 - \mu_2)}{\sqrt{S_p^2(1/n_1 + 1/n_2)}} \sim t(n_1+n_2-2)$$
$$\sigma_1^2\neq\sigma_2^2\ -\ T=\frac{(\bar X_1 - \bar X_2)-(\mu_1 - \mu_2)}{\sqrt{S_1^2/n_1 + S_2^2/n_2}} \sim t(u^*)$$
- 가중평균 : 집단의 개수가 다르면 가중치를 대입하여 평균 - $n_1 \bar x_1 + n_2 \bar x_2 \over n_1 + n_2$
- 합동분산 $S_p^2 = \frac{(n_1-1)S_1^2+(n_2-1)S_2^2}{(n_1-1)+(n_2-1)}$ - S는 자유도가 1
- $u^*$는 실수
가설
$$H_0 : \mu_1-\mu_2=0$$
등분산 검정
가설
$$H_0 : \frac{\sigma_1^2}{\sigma_2^2}=1,\ \sigma_1^2=\sigma_2^2$$
- 분산의 비는 F분포
- 우단측 검정만 실행
- 큰 $\sigma$를 위에
Example 1
등분산 검정
$$H_0 : \frac{\sigma_1^2}{\sigma_2^2}=1$$
1 | > var.test(mpg~am,mtcars) |
var.test(수치~범주,Data)- $p=0.06691 \geq 0.05$이므로 귀무가설 채택
- $\sigma_1^2=\sigma_2^2$
독립표본 T-검정(등분산)
$$H_0 : \mu_1-\mu_2=0$$
1 | > t.test(mpg~am,mtcars,var.equal=T) |
- $p=0.000285 \leq 0.05$이므로 귀무가설 기각
- $\mu_1 \neq \mu_2$
해석
group 1의 평균은 24.39231,group 0의 평균은 17.14737으로group 1의 평균이 더 크다.
Example 2
등분산 검정
$$H_0 : \frac{\sigma_1^2}{\sigma_2^2}=1$$
1 | > var.test(Price~Origin,Cars93) |
- $p=0.01387 \leq 0.05$이므로 귀무가설 기각
- $\sigma_1^2 \neq \sigma_2^2$
독립표본 T-검정(이분산)
$$H_0 : \mu_1-\mu_2=0$$
1 | > t.test(Price~Origin,Cars93,var.equal=F) |
- $p=0.3428 \geq 0.05$이므로 귀무가설 채택
- $\mu_1=\mu_2$
해석
USA와non-USA의Price차이는 없다.
Example 3
1 | > var.test(Weight~Origin,Cars93) |
해석
USA의 차가Weight즉, 무게가non-USA의 차보다 더 나간다.
대응표본 T-검정
수치자료 2개 - 전후비교
검정통계량
$$T=\frac{\bar D - \mu_D}{S_D/\sqrt{n}} \sim t(n-1)$$
가설
$$H_0 : \mu_{before}-\mu_{after}=\mu_D=0$$
Example
$$H_0 : \mu_{before}-\mu_{after}=\mu_D=0$$
1 | > attach(shoes) |
- $p=0.008539\leq0.05$이므로 귀무가설 기각
- $\mu_A\neq \mu_B$
해석
- 평균적으로
A가B보다 0.41 작다.
일원배치 분산분석
집단 N개, 수치자료 1개 - N개 집단 평균비교($N \geq 3$)
검정통계량
$$F=\frac{S_1^2}{S_2^2}=\frac{MSB}{MSW}$$
가설
$$H_0 : \mu_1 = \mu_2 = … = \mu_k$$
$$H_1 : \mu_j(적어도\ 하나)는\ 같지\ 않다$$
분산
$$S^2=\frac{1}{n-1}\sum(x_i-\bar x)^2$$
- 편차의 제곱합
- 자유도로 나눔
- 평균제곱합
$$Y_{ij}$$
- i번째 집단 j번째 Data
$$Y_{ij}-\bar Y=(\bar Y_i-\bar Y)+(Y_{ij}-\bar Y_i)$$
$$(Y_{ij}-\bar Y)^2=(\bar Y_i-\bar Y)^2+(Y_{ij}-\bar Y_i)^2$$
$$\sum_i \sum_j (Y_{ij}-\bar Y)^2=\sum_i \sum_j (\bar Y_i-\bar Y)^2+\sum_i \sum_j (Y_{ij}-\bar Y_i)^2$$
$$총제곱합(Sum\ of\ Square\ Total)=집단간\ 제곱합(Sum\ of\ Square\ Between)+집단내\ 제곱합(Sum\ of\ Square\ Within)$$
$$df : n-1=(k-1)+(n-k)$$
k- 집단수
다중비교
- 귀무가설을 기각할때 차이가 있는지 여부만 알고 어떻게 차이가 있는지 알지 못함
- 따라서 다중비교, 하지만 분산분석과는 별개
Tukey - HSD(Honest Significant Difference) 방법
- 가장 보수적
분산분석표 분석
- SSB
- SSW
- df
Example
$$H_0 : \mu_1 = \mu_2 = … = \mu_k$$
1 | > a=lm(Price~DriveTrain,Cars93);a |
DriveTrain집단간,Residual집단내- $p=4.202 \times 10^{-5} \leq 0.05$이므로 귀무가설 기각
- 각 집단의 평균이 차이를 보임
다중비교
1 | > a1=aov(Price~DriveTrain,Cars93);a1 |
해석
- 후륜구동 자동차가 4륜, 전륜에 비해 비싼 가격을 가지는 경향을 보임
- 4륜과 전륜 자동차는 비슷한 가격을 가지는 경향을 보임
회귀분석
$$Y_i(종속)=\beta_0+\beta_1x_i(독립)+\epsilon_i$$
$$\epsilon_i(오차항) \sim N(0,\sigma^2) - 확률변수$$
- 오차항(회귀분석은 아래 가정을 따라야 함)
- 정규성
- 독립성
- 등분산성
- 독립변수 -> 종속변수 영향력? - $\beta_1$
- $\beta_0, \beta_1$ - 모수(상수)
- $E(Y_i)=\beta_0+\beta_1x_i$
- $V(Y_i)=\sigma^2$
$$Y_i \sim N(\beta_0+\beta_1x_i,\sigma^2)$$
$$D=\sum_{i=1}^ne_i=\sum_{i=1}^n(Y_i-\hat{Y_i})^2=\sum_{i=1}^n(Y_i-y(x_i))^2$$
- $e_i$ - Residual(잔차)
- $\hat{Y_i}$ - 추정량(예측치)
검정통계량
F-검정
$$MSR=\frac{SSR}{k},\ MSE=\frac{SSE}{n-k-1}$$
$$F=\frac{MSR}{MSE}$$
T-검정
$$T=\frac{\hat{\beta_1}-\beta_1}{\sqrt{\frac{MSE}{\sum(x_i-\bar{x})^2}}} \sim t(n-2)$$
F는 모든 계수 검정,T는 $\beta_1$만 검정
가설
F-검정
$$H_0 : \beta_1 = 0(회귀모형\ 적합\ X)$$
T-검정
$$H_0 : \beta_0=0, T=\frac{\hat{\beta_0}-\beta_0}{\sqrt{MSE(\frac{1}{n}+\frac{\bar{x}^2}{\sum(x_i-\bar{x})^2})}}\sim t(n-2)$$
$$H_0 : \beta_1=0, T=\frac{\hat{\beta_1}-\beta_1}{\sqrt{\frac{MSE}{\sum(x_i-\bar{x})^2}}} \sim t(n-2)$$
Least squares regression
$$\frac{\partial D}{\partial \hat \beta_0}=0$$
$$\frac{\partial D}{\partial \hat \beta_1}=0$$
$\hat \beta_0,\ \hat \beta_1$의 분포
$$\hat{\beta_0}=\bar{Y}-\hat{\beta_1}\bar{x} \sim N(\beta_0,\sigma^2(\frac{1}{n}+\frac{\bar{x}^2}{\sum(x_i-\bar{x})^2})$$
$$\hat{\beta_1}=\frac{\sum(x_i-\bar{x})(Y_i-\bar{Y})}{\sum(x_i-\bar{x})^2} \sim N(\beta_1,\frac{\sigma^2}{\sum(x_i-\bar{x})^2})$$
분산분석
$$Y_{i}-\bar Y=(\hat Y_i-\bar Y)+(Y_{i}-\hat Y_i)$$
$$\sum (Y_{i}-\bar Y)^2=\sum (\hat Y_i-\bar Y)^2+\sum (Y_{i}-\hat Y_i)^2$$
$$총제곱합(SST)=회귀제곱합(SSR)+잔(오)차제곱합(SSE)$$
$$df : n-1=(k)+(n-k-1)$$
SSR은 크고SSE는 작아야 유리k- 독립변수 개수
$R^2$ - 결정계수
$$R^2=\frac{SSR}{SST}$$
- 설명력
- 높을수록 좋음
진행 순서
plot(param1,param2)- 산점도 확인name=lm(param2~param1,Data)- Coefficient 확인anova(name)- F, SSR, SSE(Residual) 확인summary(name)- 결정계수, T 확인
Example 1
$$H_0 : \beta_1 = 0(회귀모형\ 적합\ X)$$
1 | > a=lm(Price~Length,Cars93);a |
- Length -
SSR - Residual -
SSE - $2.663 \times 10^{-7} \leq 0.05$이므로 귀무가설 기각
- $\beta_1 \neq 0$
Length의F value를 제곱하면t vlue- 약 25% 설명
Example 2
$$H_0 : \beta_1 = 0(회귀모형\ 적합\ X)$$
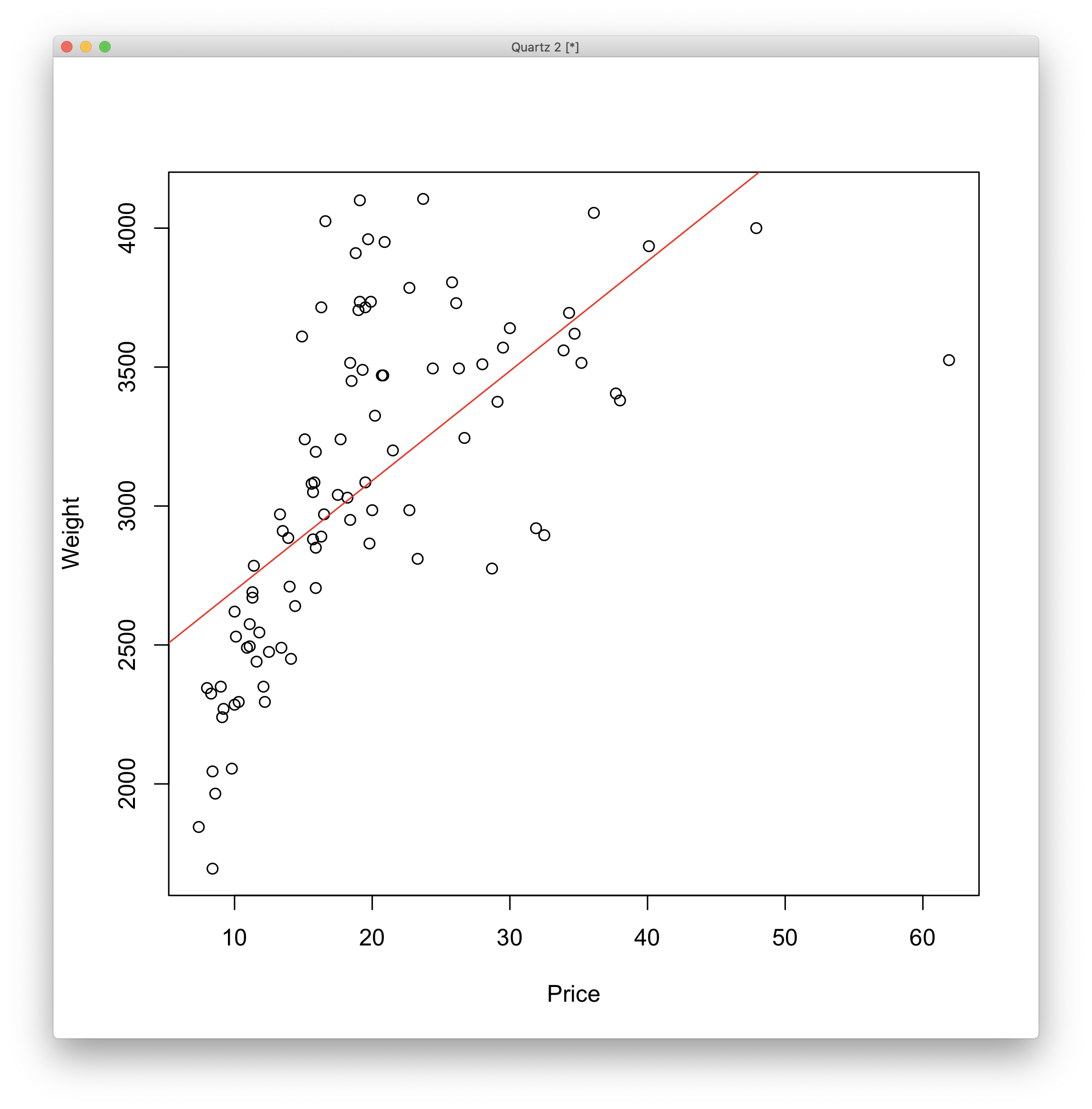
1 | > plot(Price,Weight) |
- Price -
SSR - Residual -
SSE - $2.395 \times 10^{-12} \leq 0.05$이므로 귀무가설 기각
- $\beta_1 \neq 0$
- 약 42% 설명
Example 3
$$H_0 : \beta_1 = 0(회귀모형\ 적합\ X)$$
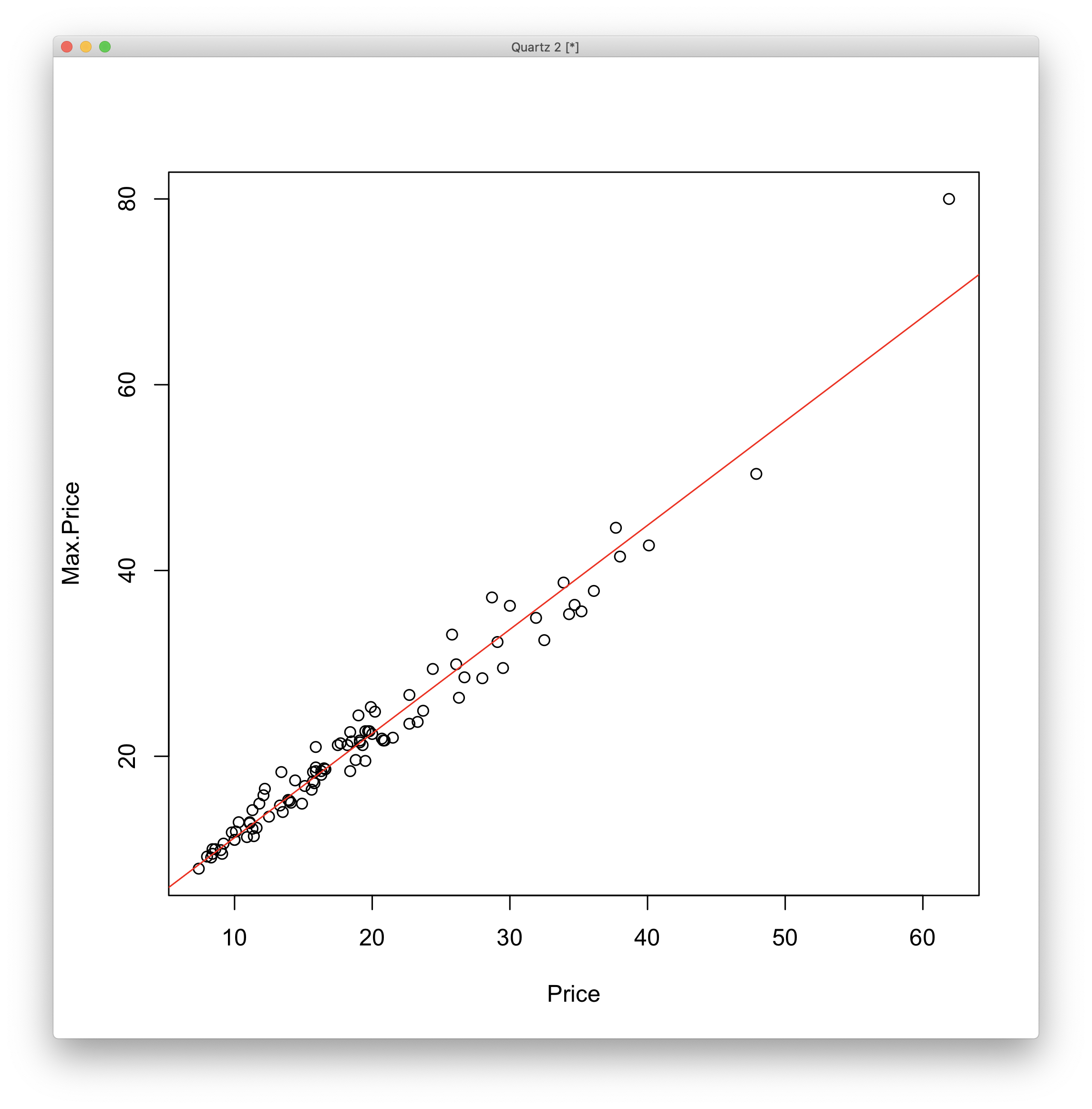
1 | > plot(Price,Max.Price) |
- Price -
SSR - Residual -
SSE - $2.2 \times 10^{-16} \leq 0.05$이므로 귀무가설 기각
- $\beta_1 \neq 0$
- 약 96% 설명
Finale
1 | go=function(a){ |
