R (6)

Posted on In

ifelse

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
> x=1
> y=2
> if(x>y) x else y
[1] 2
> if(x<y) x else y
[1] 1
> ifelse(x>y,x,y) #조건식,참x,거짓y
[1] 2
> ifelse(x<y,x,y) #조건식,참x,거짓y
[1] 1
> grade=ifelse(airquality$Temp>=60,'상','하');grade
  [1] "상" "상" "상" "상" "하" "상" "상" "하" "상" "상" "상" "상" "상" "상" "하" "상" "상" "하" "상"
...
[153] "상"
> air0=data.frame(airquality,grade);air0
    Ozone Solar.R Wind Temp Month Day grade
1      41     190  7.4   67     5   1    상
2      36     118  8.0   72     5   2    상
3      12     149 12.6   74     5   3    상
4      18     313 11.5   62     5   4    상
5      NA      NA 14.3   56     5   5    하
6      28      NA 14.9   66     5   6    상
7      23     299  8.6   65     5   7    상
8      19      99 13.8   59     5   8    하
9       8      19 20.1   61     5   9    상
10     NA     194  8.6   69     5  10    상
...
> airquality$grade=ifelse(airquality$Temp>=60,'상','하');airquality
    Ozone Solar.R Wind Temp Month Day grade
1      41     190  7.4   67     5   1    상
2      36     118  8.0   72     5   2    상
3      12     149 12.6   74     5   3    상
4      18     313 11.5   62     5   4    상
5      NA      NA 14.3   56     5   5    하
6      28      NA 14.9   66     5   6    상
7      23     299  8.6   65     5   7    상
8      19      99 13.8   59     5   8    하
9       8      19 20.1   61     5   9    상
10     NA     194  8.6   69     5  10    상
...
  • 두가지만 간단히 있을시 사용

switch문

1
2
3
4
5
6
7
8
9
10
11
12
13
14
> score=c(80,75,40,98)
> for(i in c(3,1,2)){
+ 	print(switch(i,mean(score),median(score),sd(score)))
+ }
[1] 24.26761
[1] 73.25
[1] 77.5
> type=c('mean','sd')
> for(i in type){
+ 	res=switch(i,mean=mean(score),sd=sd(score))
+ 	cat(i,res,'\n')
+ }
mean 73.25 
sd 24.26761
  • 별로 안쓰임

function

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
> attach(Cars93)
> plot(Length,Width)
> library(MASS)
> str(Cars93)
'data.frame':	93 obs. of  27 variables:
 $ Manufacturer      : Factor w/ 32 levels "Acura","Audi",..: 1 1 2 2 3 4 4 4 4 5 ...
 $ Model             : Factor w/ 93 levels "100","190E","240",..: 49 56 9 1 6 24 54 74 73 35 ...
...
 $ Make              : Factor w/ 93 levels "Acura Integra",..: 1 2 4 3 5 6 7 9 8 10 ...
> attach(Cars93)
> plot(Length,Width)
> cor(Length,Width)
[1] 0.8221479
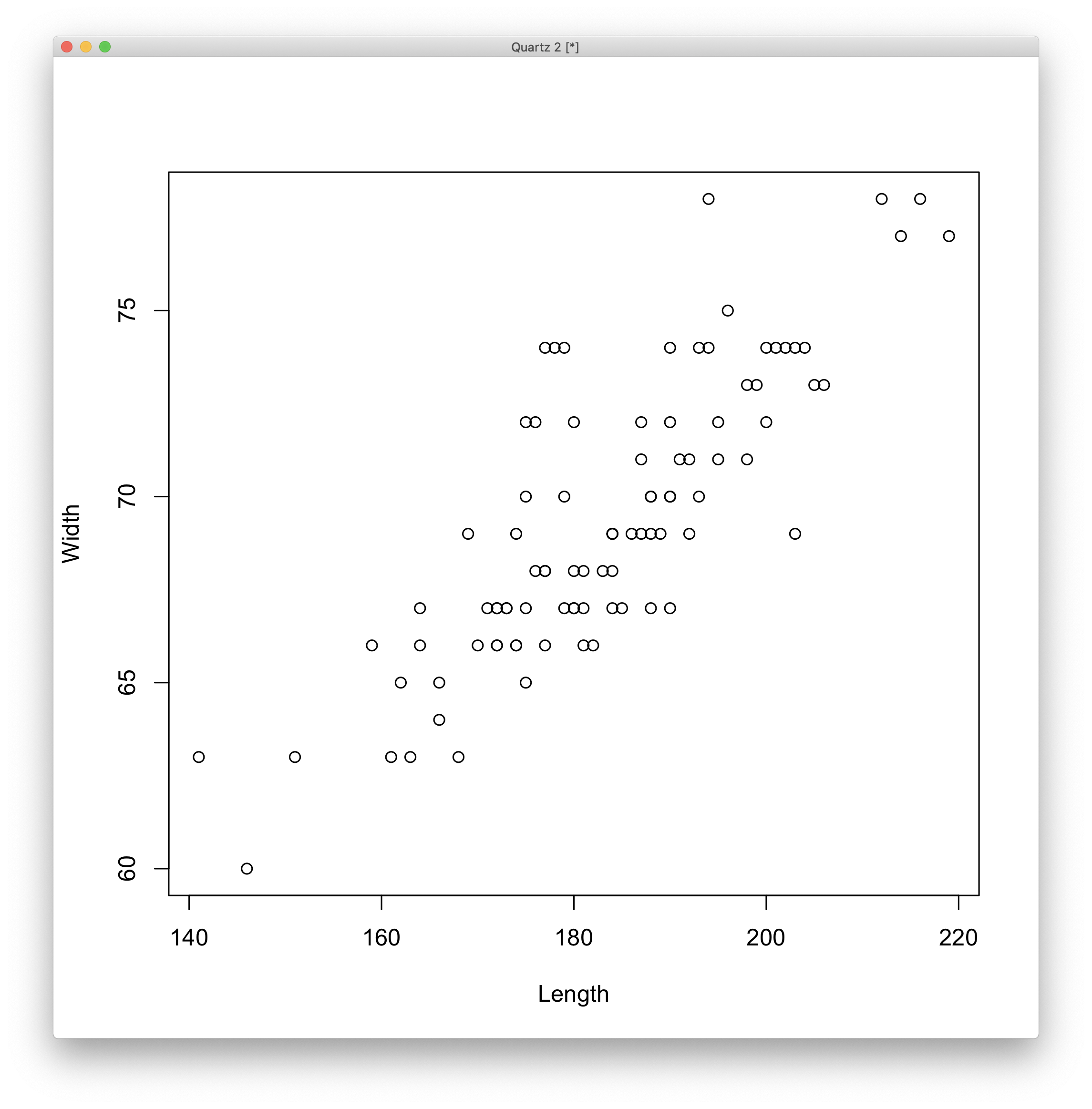
> Z_Score=function(x){ #Normalize
+ 	Z=((x-mean(x))/sd(x))
+ 	return(Z)
+ }
> Z_Score(Length)
 [1] -0.42488282  0.80779282 -0.21943688  0.67082886  0.19145500  0.39690094  1.15020272  2.24591440
...
[89]  0.25993698 -0.21943688 -1.65755846  0.46538292  0.05449104
> a=Cars93
> Z_Score=function(x){ #Normalize
+ 	a$Z<<-((x-mean(x))/sd(x))
+ }
> Z_Score(Length)
> str(a)
'data.frame':	93 obs. of  28 variables:
 $ Manufacturer      : Factor w/ 32 levels "Acura","Audi",..: 1 1 2 2 3 4 4 4 4 5 ...
...
 $ Z                 : num  -0.425 0.808 -0.219 0.671 0.191 ...

  • 함수의 변수는 지역변수
  • 전역변수는 <<-로 설정
  • Normalize는 scale()도 가능

with()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
> with(Cars93,mean(Cars93$Length))
[1] 183.2043
> with(Cars93,mean(Length))
[1] 183.2043
> mean(Cars93$Length)
[1] 183.2043
> with(Cars93,c(mean(Length),sd(Length)))
[1] 183.20430  14.60238
> 
> dif=function(x){
+ 	d=(x-mean(x))
+ 	return(d)
+ }
> with(Cars93,dif(Length))
 [1]  -6.2043011  11.7956989  -3.2043011   9.7956989   2.7956989   5.7956989  16.7956989  32.7956989
...
[89]   3.7956989  -3.2043011 -24.2043011   6.7956989   0.7956989
> dif(Length) #attach
...
[89]   3.7956989  -3.2043011 -24.2043011   6.7956989   0.7956989
> dif(Cars93$Length)
 [1]  -6.2043011  11.7956989  -3.2043011   9.7956989   2.7956989   5.7956989  16.7956989  32.7956989
...
[89]   3.7956989  -3.2043011 -24.2043011   6.7956989   0.7956989

왜도(Skewness) - skew()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
> skew1=function(x){
+ 	sk=sum(((x-mean(x))^3)/sd(x)^3)*(1/(length(x)-1))
+ 	return(sk)
+ }
> 
> library(psych)
> skew(Length)
[1] -0.08720918
> skew1(Length)
[1] -0.0881571
> skew1=function(x){
+ 	sk=sum(((x-mean(x))^3)/sd(x)^3)*(1/(length(x)))
+ 	return(sk)
+ }
> skew1(Length)
[1] -0.08720918


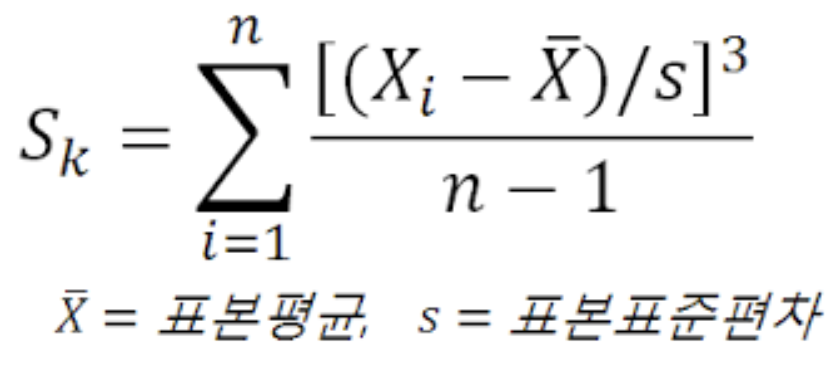
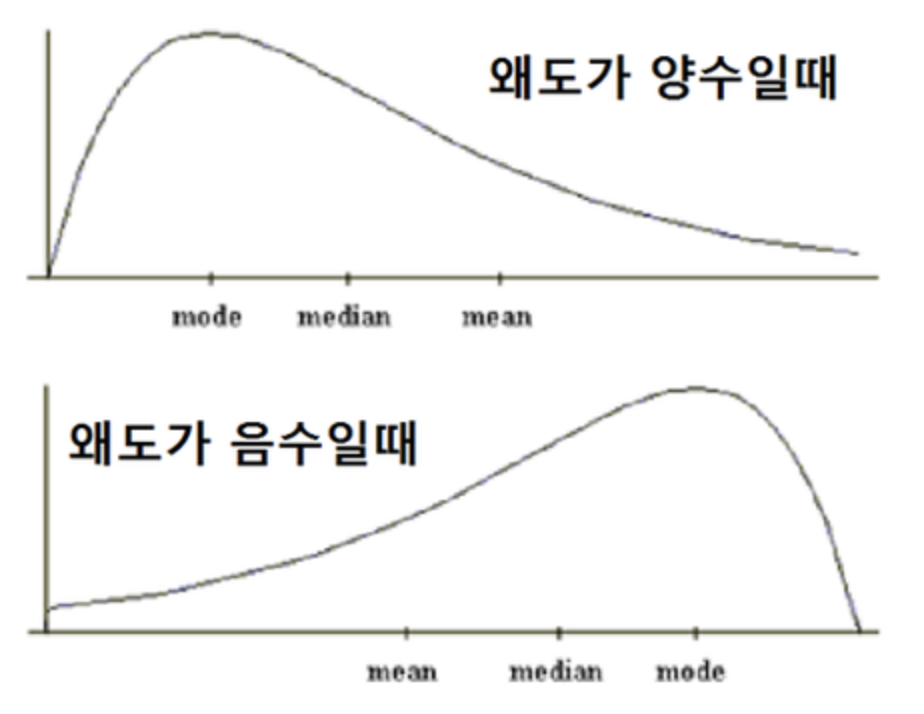
  • nrow(), ncol() - Matrix, data.frame
  • length() - Vector

첨도(Kurtosis) - kurtosi()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
> kur=function(x){
+ 	ku=sum(((x-mean(x))^4)/sd(x)^4)*(1/(length(x)-1))
+ 	return(ku)
+ }
> 
> kurtosi(Length)
[1] 0.2897238
> kur(Length)
[1] 3.325482
> kur(Length)-3
[1] 0.3254817
> kur=function(x){
+ 	ku=sum(((x-mean(x))^4)/sd(x)^4)*(1/(length(x)))
+ 	return(ku)
+ }
> kur(Length)
[1] 3.289724
> kur(Length)-3
[1] 0.2897238

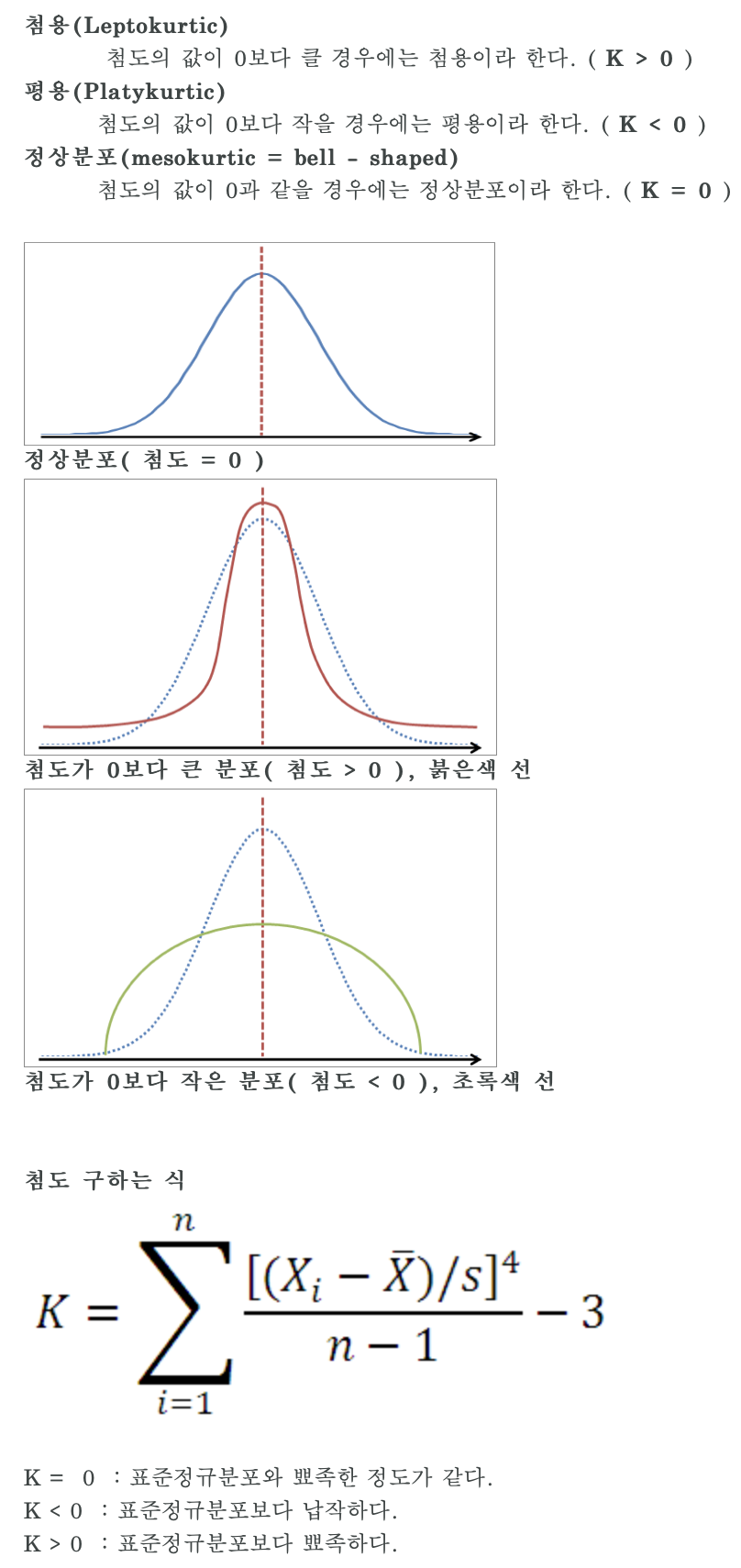
  • 정규분포는 왜도가 0 첨도가 3
  • 첨도는 기준을 0 or 3 - 이론은 무조건 3 기준
  • kurtosi() < 3 - 완첨
  • kurtosi() = 3 - 중첨
  • kurtosi() > 3 - 급첨

기술통계학

  • 자료 요약 및 정리 : 표(도수분포표)와 그래프()

  • 범주형 - 도수분포표(빈도를 그래프로 할 수 있긴 함)

  • 수치형 - 기술통계량(분포의 특성)

    • 대표값(중심위치)
      • 산술평균
      • 중위수
      • 최빈수(보통 범주형에서 사용, 수치형에선 이산형에서 가끔)
    • 산포도(흩어진 정도)
      • 표준편차(기존단위가 같음)
      • 분산(단위^2)
      • 변이(변동)계수(CV) : sd()/mean()
      • 사분위수범위(Q3-Q1) : boxplot()
    • 비대칭도
      • 왜도

  • 오류데이터 찾기

    • 최소값
    • 최대값
    • 도수분포표
    • summary()

  • 관련된 변수 2개

    • 수치형 2개 : cor(name1,name2)
    • 범주형 2개 : 교차표(분할표)

  • 외부파일 읽기(.txt) - read.table() / read.csv() - str() - summary()

    • Data 여러개 - Data handling
      • 병합
        • rbind - 행(Case) 추가
        • cbind - 열(변수) 추가
      • 새로운 변수 생성
        • 변수계산 : 기존 변수를 가지고 계산을 통해 새로운 변수 생성
        • 코딩변경 : 기존 변수를 가지고 새로운 변수 생성(Ex. 학점 예제) - 보통 범주형
      • 데이터 취사선택 : indexing - [], subset()
      • 정렬 : sort(), order()

  • Slicing : substr()

  • NA : mean(name,na.rm=T)

  • 출력 : cat(), sink(), pdf(), dev.off()

  • 연산자, 제어문(반복문, 조건문), 함수

단위계산은 *, /만 계산

변동계수

  • 평균의 차가 많은 집단끼리의 산포도 비교시 사용
  • 단위가 다른 변수에 대한 산포도 비교 - 무차원수
  • 극심한 비대칭일때 사용
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
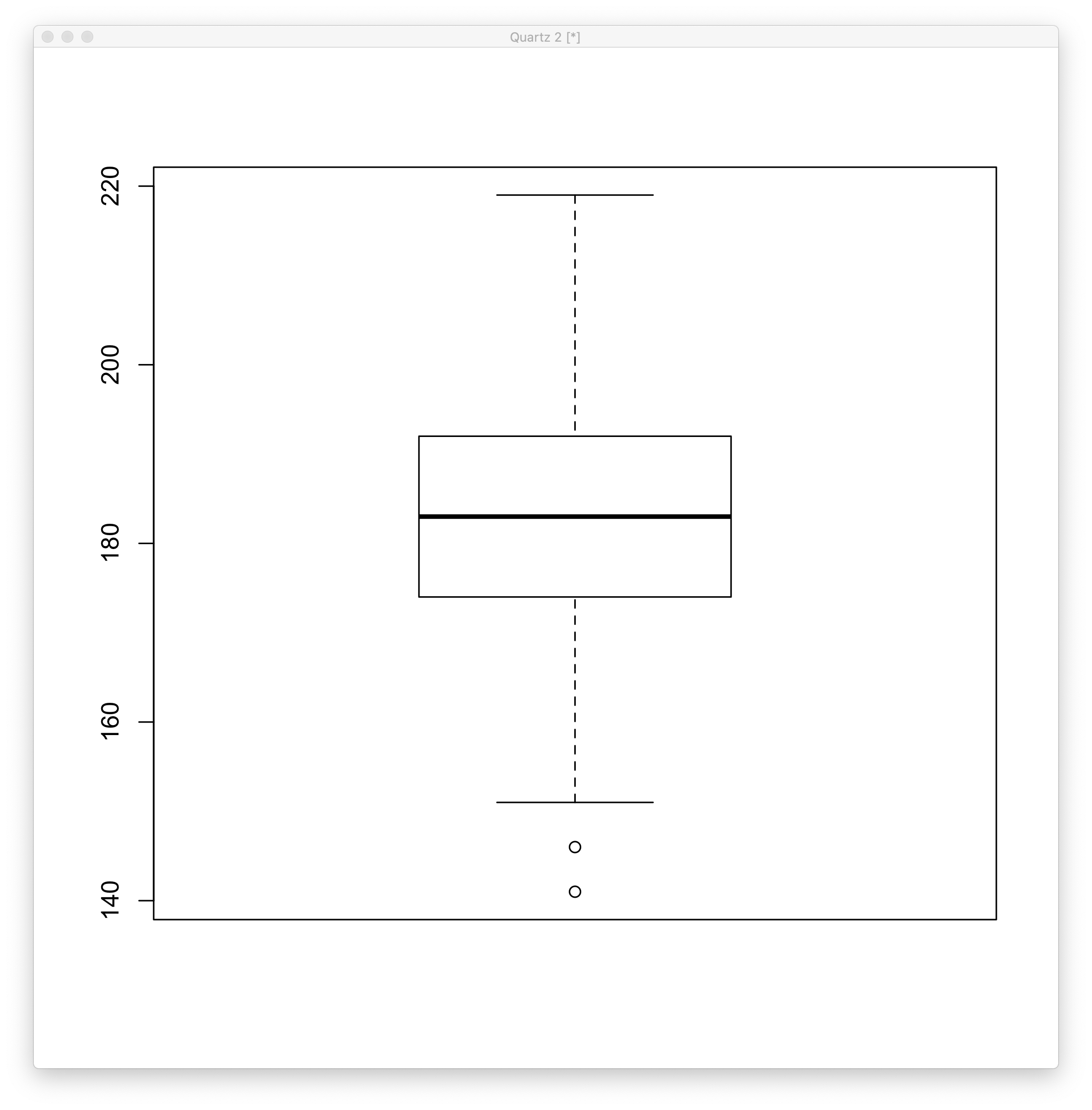
> boxplot(Length)
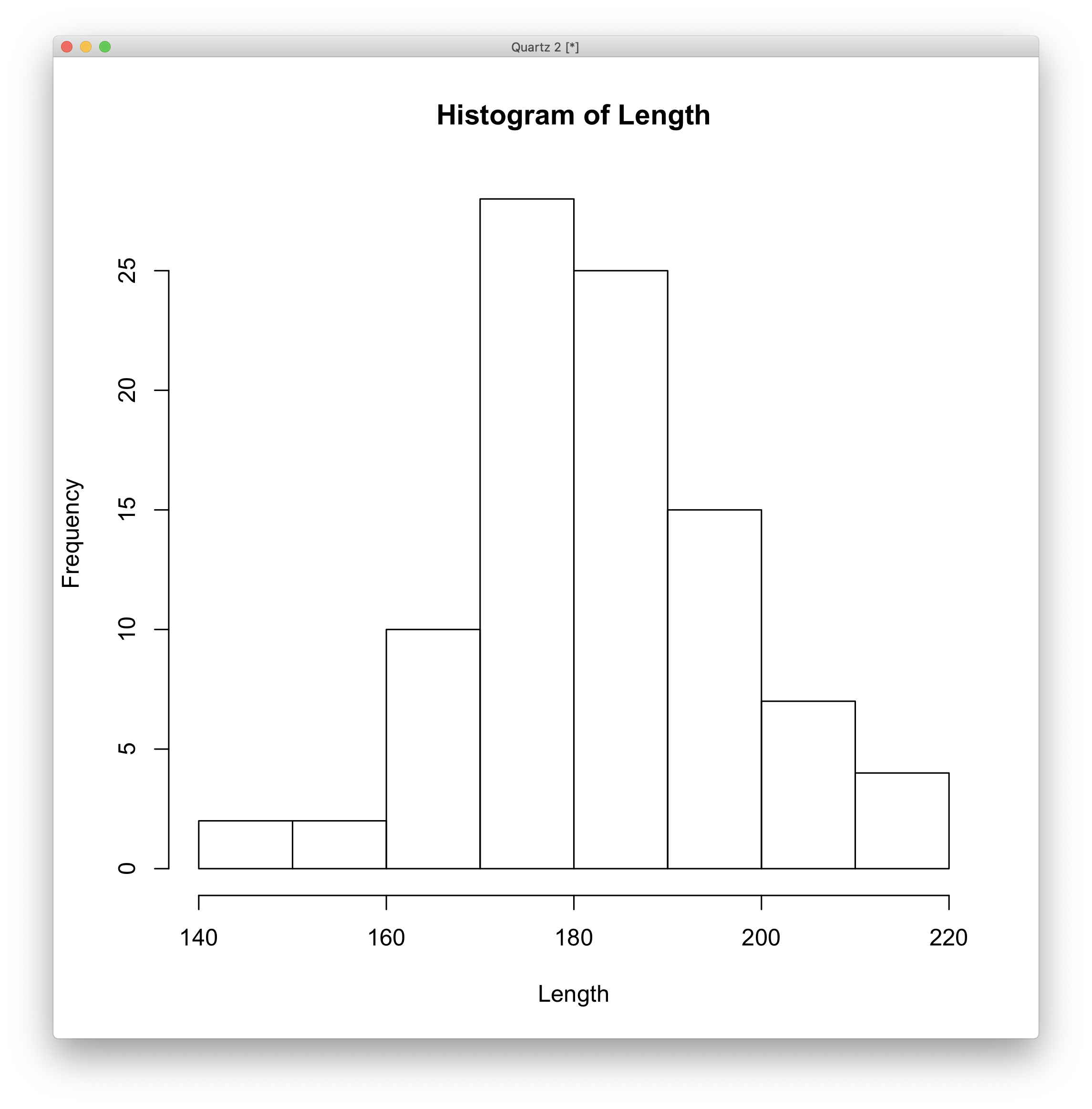
> hist(Length)
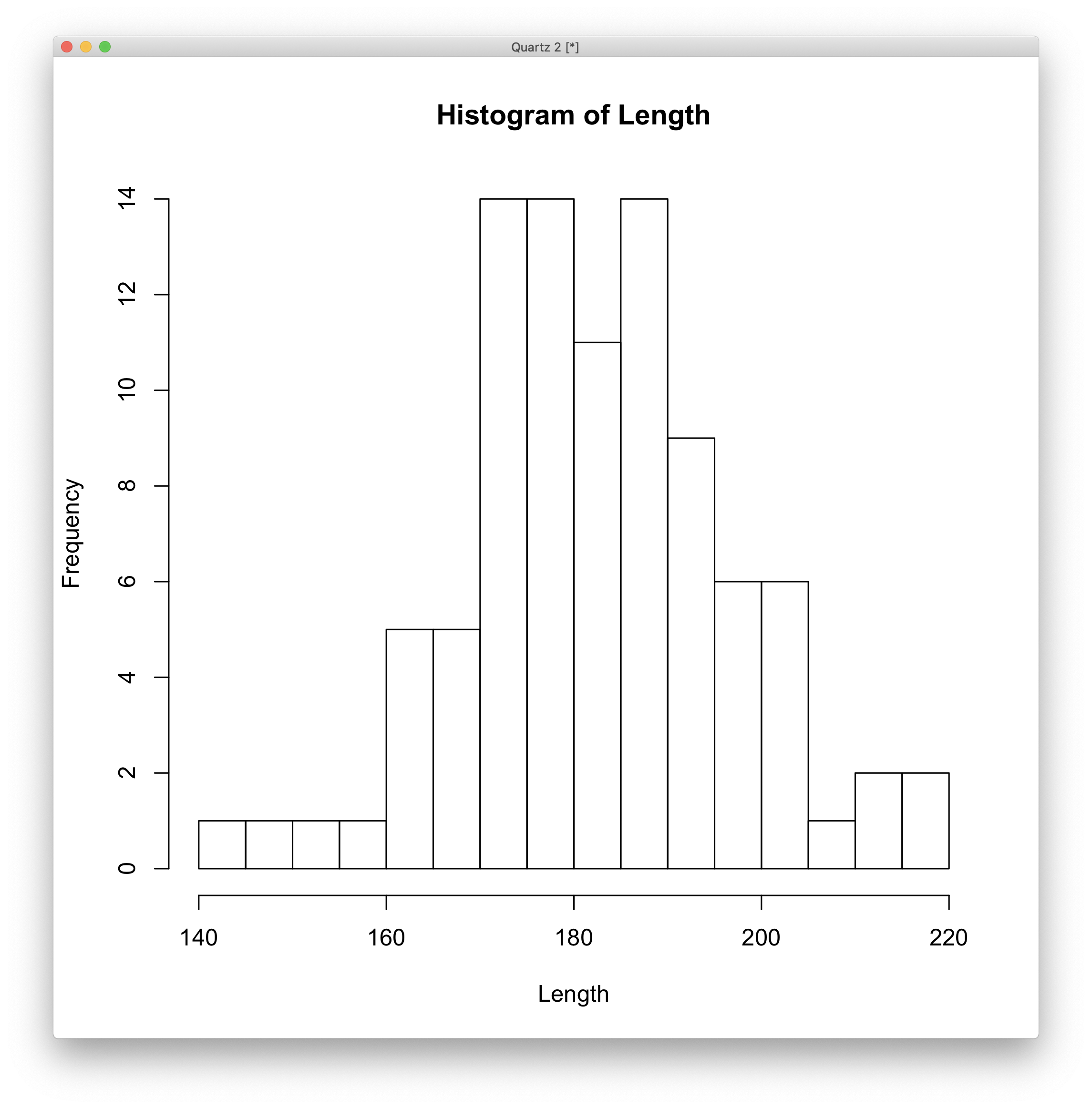
> hist(Length,nclass=16)
> stem(Length)

  The decimal point is 1 digit(s) to the right of the |

  14 | 16
  15 | 19
  16 | 123446689
  17 | 0122223344455556677778999
  18 | 000011123444445677788889
  19 | 000001223344556889
  20 | 001233456
  21 | 2469
> stem(Length,scale=2)

  The decimal point is 1 digit(s) to the right of the |

  14 | 1
  14 | 6
  15 | 1
  15 | 9
  16 | 12344
  16 | 6689
  17 | 01222233444
  17 | 55556677778999
  18 | 00001112344444
  18 | 5677788889
  19 | 000001223344
  19 | 556889
  20 | 0012334
  20 | 56
  21 | 24
  21 | 69
> stem(Length,scale=0.5)

  The decimal point is 1 digit(s) to the right of the |

  14 | 1619
  16 | 1234466890122223344455556677778999
  18 | 000011123444445677788889000001223344556889
  20 | 0012334562469
> cor(Length,Width)
[1] 0.8221479

boxplot(Length)
hist(Length)
hist(Length,nclass=16)

기말

확률변수, 확률분포(이산형, 연속형), 표본분포, 가설검정, 통계분석기법