Numerical Analysis (5)

Posted on In

Runge-Kutta Method for ODE

Process

  • Heun’s Method(a(2)=1/2)
  • Ralston’s Method(a(2)=2/3)
  • y(i+1)=y(i)+(a(1)k(1)+a(2)k(2))h
  • k(1)=f(x(i), y(i))
  • k(2)=f(x(i)+p(1)h, y(i)+q(11)k(1)h)

Source code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
import plotly
from plotly.graph_objs import Scatter, Layout

def f(t): #Defining dy/dt
    return - t + t**2

def Hyip1(t): #Defining y sub i+1 in Heun's Method
    return Hyi + (1/2 * Hk1 + 1/2 * Hk2) * h

def Ryip1(t): #Defining y sub i+1 in Ralston's Method
    return Ryi + (1/3 * Rk1 + 2/3 * Rk2) * h

Hyi = 1 #Defining y sub i in Heun's Method
Ryi = 1 #Defining y sub i in Ralston's Method
Ht = 0 #Defining initial value t in Heun's Method
Rt = 0 #Defining initial value t in Ralston's Method
h = 0.1 #Defining h
Hyisav = [] #Defining y sub i in Heun's Method to save
Ryisav = [] #Defining y sub i in Ralston's Method to save
Htsav = [] #Defining initial value t in Heun's Method to save
Rtsav = [] #Defining initial value t in Ralston's Method to save

while(Ht <= 3):
    Ht = round(Ht, 2)
    Hk1 = round(f(Ht), 2)  #Defining k sub 1 in Heun's Method
    Hk2 = round(f(Ht + h), 2) #Defining k sub 2 in Heun's Method
    Hyi = round(Hyip1(Ht), 2) #Determine new y sub i in Heun's Mthod
    Hyisav = Hyisav + [Hyi]
    Htsav = Htsav + [Ht]
    Ht = Ht + h #Redefining time

while(Rt <= 3):
    Rt = round(Rt, 2)
    Rk1 = round(f(Rt),)  #Defining k sub 1 in Ralston's Method
    Rk2 = round(f(Rt + 3 / 4 * h), 2)  #Defining k sub 2 in Ralston's Method
    Ryi = round(Ryip1(Rt), 2) #Determine new y sub i in Ralston's Mthod
    Ryisav = Ryisav + [Ryi]
    Rtsav = Rtsav + [Rt]
    Rt = Rt + h #Redefining time

plotly.offline.plot({ #Data ploting
    "data": [Scatter(x = Htsav, y = Hyisav)],
    "layout": Layout(title="Heun's Method")
})

plotly.offline.plot({ #Data ploting
    "data": [Scatter(x = Rtsav, y = Ryisav)],
    "layout": Layout(title="Ralston's Method")
})

print(Htsav)
for a in range(0, len(Hyisav)):
    print(Hyisav[a], end=" ")

print("\n")

print(Rtsav)
for a in range(0, len(Ryisav)):
    print(Hyisav[a], end=" ")

실행결과

1
2
3
4
5
6
7
"C:\Users\s_oh3417\PycharmProjects\수치 Proj4\venv\Scripts\python.exe" "C:/Users/s_oh3417/PycharmProjects/수치 Proj4/Main.py"
[0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0, 1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 1.9, 2.0, 2.1, 2.2, 2.3, 2.4, 2.5, 2.6, 2.7, 2.8, 2.9, 3.0]
1.0 0.99 0.97 0.95 0.93 0.91 0.89 0.87 0.86 0.86 0.87 0.89 0.92 0.97 1.04 1.13 1.24 1.37 1.53 1.72 1.94 2.19 2.47 2.79 3.15 3.55 3.99 4.47 5.0 5.58 6.21 

[0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0, 1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 1.9, 2.0, 2.1, 2.2, 2.3, 2.4, 2.5, 2.6, 2.7, 2.8, 2.9, 3.0]
1.0 0.99 0.98 0.96 0.94 0.92 0.91 0.9 0.89 0.89 0.9 0.91 0.93 0.96 1.04 1.13 1.24 1.37 1.51 1.71 1.93 2.17 2.46 2.78 3.12 3.52 3.95 4.45 4.98 5.57 6.2 
Process finished with exit code 0

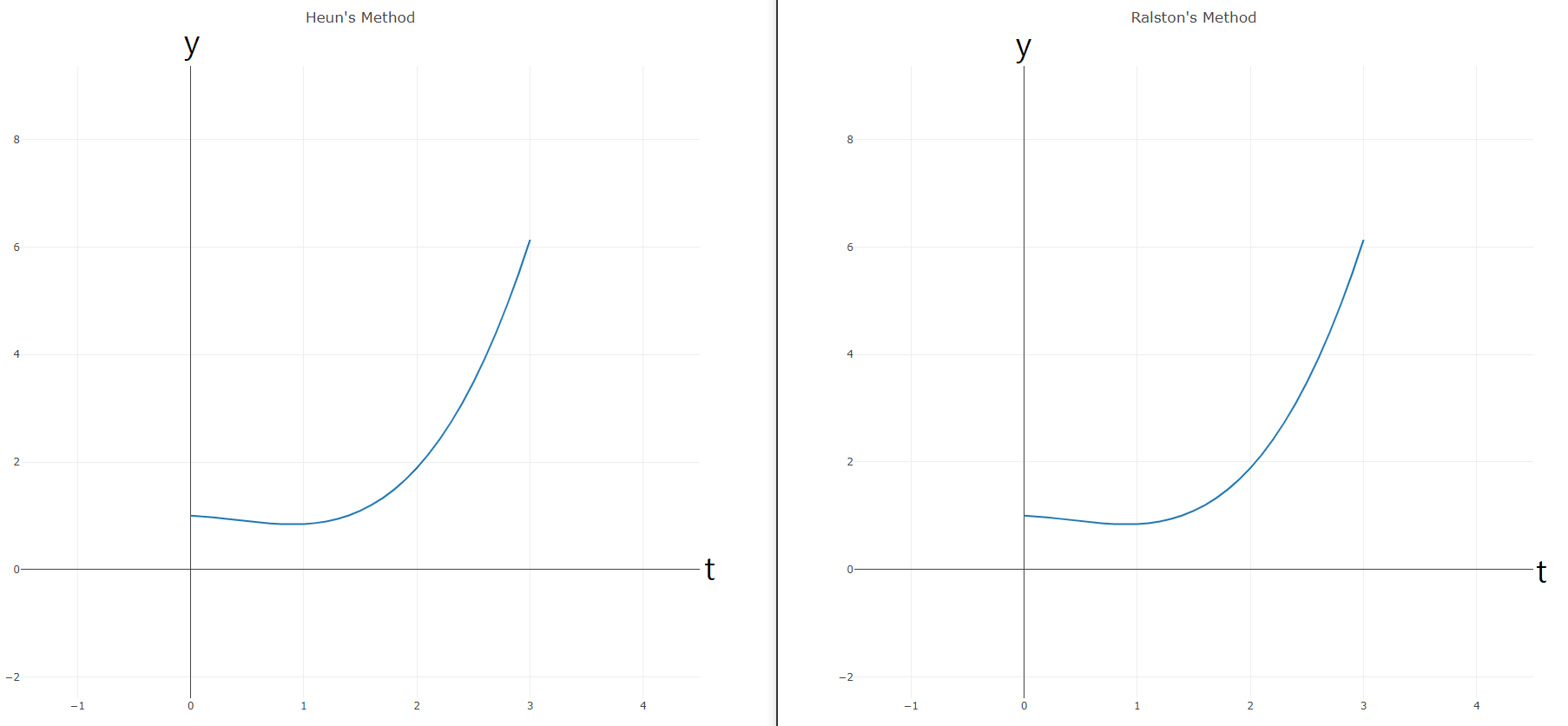
result-1
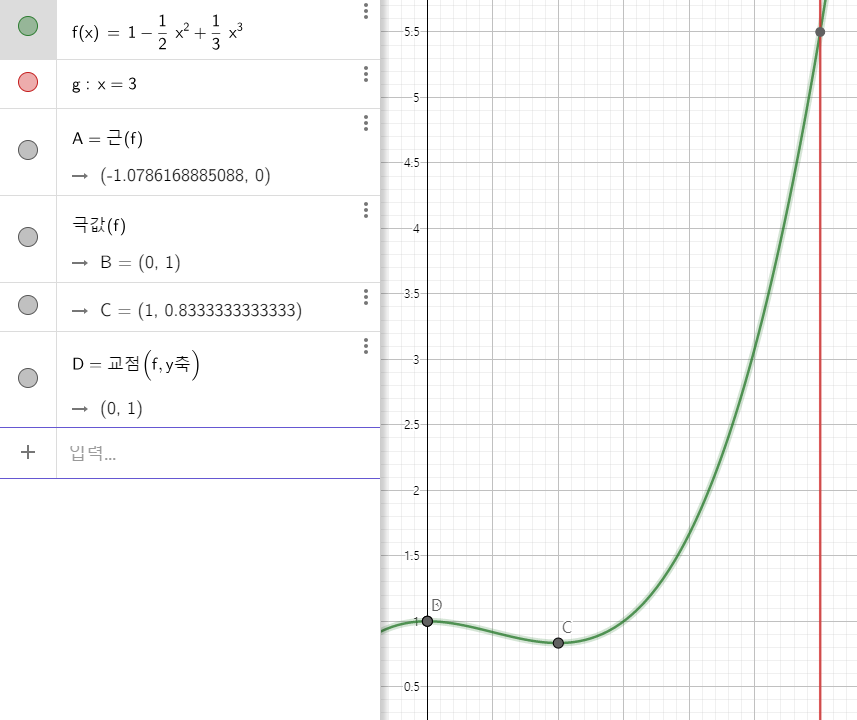
solution-of-ode

데이터 비교

1
2
3
4
5
x = 0:0.1:3;
y1 = 1-1/2*x.^2+1/3*x.^3;
y2 = [1 0.99 0.97 0.95 0.93 0.91 0.89 0.87 0.86 0.86 0.87 0.89 0.92 0.97 1.04 1.13 1.24 1.37 1.53 1.72 1.94 2.19 2.47 2.79 3.15 3.55 3.99 4.47 5.0 5.58 6.21]
y3 = [1.0 0.99 0.98 0.96 0.94 0.92 0.91 0.9 0.89 0.89 0.9 0.91 0.93 0.96 1.04 1.13 1.24 1.37 1.51 1.71 1.93 2.17 2.46 2.78 3.12 3.52 3.95 4.45 4.98 5.57 6.2]
plot(x,y1,x,y2,x,y3)

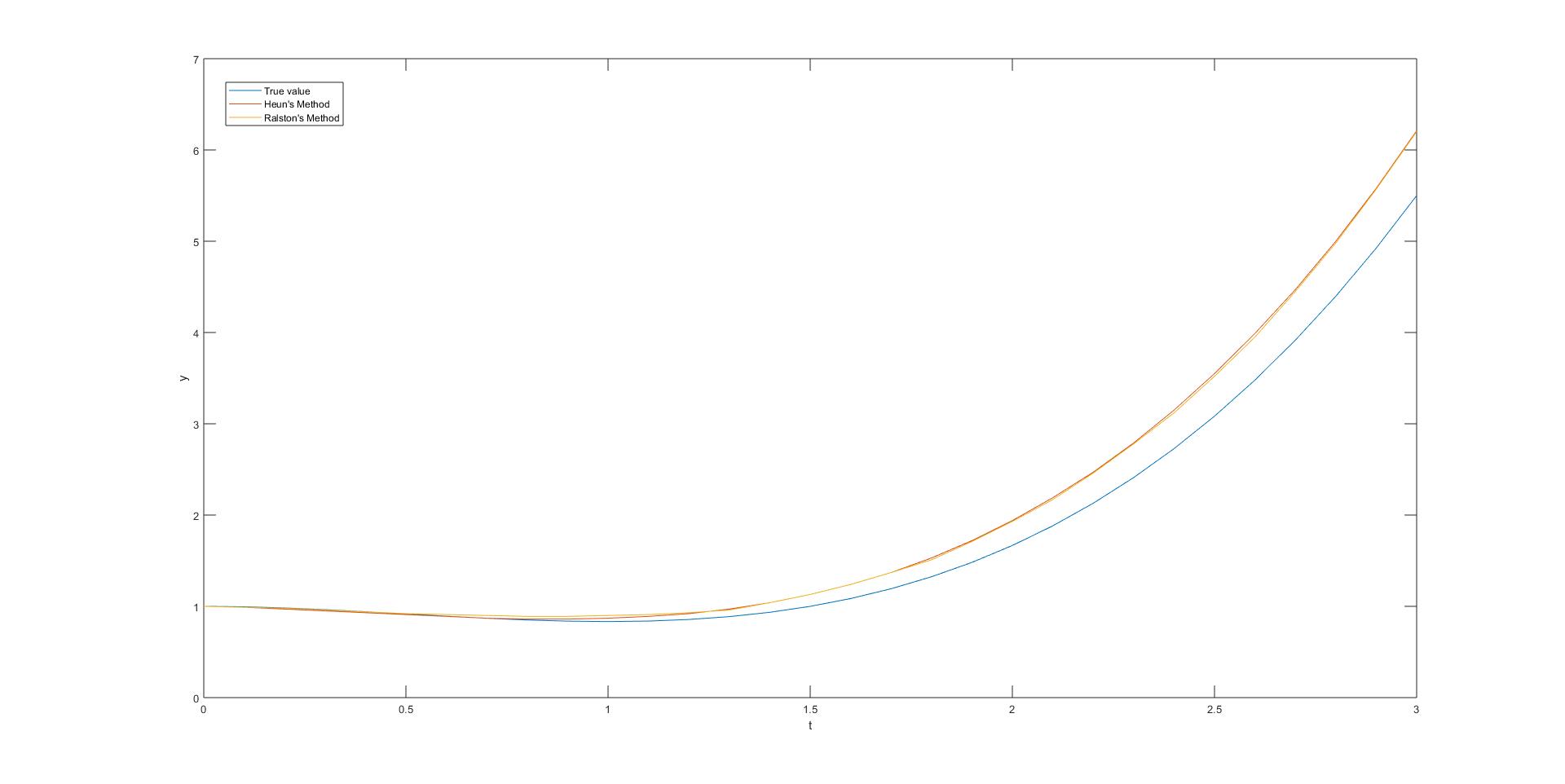
result-2

Discussion

오차가 가장 큰 t=3인 지점의 참값은 5.5이지만 Heun’s Method와 Ralston’s Method를 통한 값은 각각 6.21, 6,2이다. 이는 각각 0.71, 0.7이라는 값이 차이난다는 것이고 미세하게 Ralston’s Method가 더 정교함을 울 수 있다. 또한 이 정도의 오차가 발생한 이유를 생각해보면, h값이 0.1로 꽤나 큰 수치이기 때문일 것이다. 그럼에도 불구하고 약 t=1.2까지는 True value와 거의 같다고 볼 수 있다. h가 작아지면 충분히 같아질 것이다.

호기심 해결

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
import plotly
from plotly.graph_objs import Scatter, Layout

def f(t): #Defining dy/dt
    return - t + t**2

def Hyip1(t): #Defining y sub i+1 in Heun's Method
    return Hyi + (1/2 * Hk1 + 1/2 * Hk2) * h

def Ryip1(t): #Defining y sub i+1 in Ralston's Method
    return Ryi + (1/3 * Rk1 + 2/3 * Rk2) * h

Hyi = 1 #Defining y sub i in Heun's Method
Ryi = 1 #Defining y sub i in Ralston's Method
Ht = 0 #Defining initial value t in Heun's Method
Rt = 0 #Defining initial value t in Ralston's Method
h = 0.0001 #Defining h
Hyisav = [] #Defining y sub i in Heun's Method to save
Ryisav = [] #Defining y sub i in Ralston's Method to save
Htsav = [] #Defining initial value t in Heun's Method to save
Rtsav = [] #Defining initial value t in Ralston's Method to save

while(Ht <= 3):
    Ht = round(Ht, 10)
    Hk1 = round(f(Ht), 10)  #Defining k sub 1 in Heun's Method
    Hk2 = round(f(Ht + h), 10) #Defining k sub 2 in Heun's Method
    Hyi = round(Hyip1(Ht), 10) #Determine new y sub i in Heun's Mthod
    Hyisav = Hyisav + [Hyi]
    Htsav = Htsav + [Ht]
    Ht = Ht + h #Redefining time
    print(Ht)

while(Rt <= 3):
    Rt = round(Rt, 10)
    Rk1 = round(f(Rt), 10)  #Defining k sub 1 in Ralston's Method
    Rk2 = round(f(Rt + 3 / 4 * h), 10)  #Defining k sub 2 in Ralston's Method
    Ryi = round(Ryip1(Rt), 10) #Determine new y sub i in Ralston's Mthod
    Ryisav = Ryisav + [Ryi]
    Rtsav = Rtsav + [Rt]
    Rt = Rt + h #Redefining time
    print(Rt)

plotly.offline.plot({ #Data ploting
    "data": [Scatter(x = Htsav, y = Hyisav)],
    "layout": Layout(title="Heun's Method")
})

plotly.offline.plot({ #Data ploting
    "data": [Scatter(x = Rtsav, y = Ryisav)],
    "layout": Layout(title="Ralston's Method")
})

print(Htsav)
for a in range(0, len(Hyisav)):
    print(Hyisav[a], end=" ")

print("\n")

print(Rtsav)
for a in range(0, len(Ryisav)):
    print(Ryisav[a], end=" ")

실행결과

1
2
2.4925, 2.4926, 2.4927, 2.4928, 2.4929, 2.493, 2.4931, 2.4932, 2.4933, 2.4934, 2.4935, 2.4936, 2.4937, 2.4938, 2.4939, 2.494, 2.4941, 2.4942, 2.4943, 2.4944, 2.4945, 2.4946, 2.4947, 2.4948, 2.4949, 2.495, ..., 5.4946022248 5.4952017999 5.495801425 5.4964011 5.497000825 5.4976006 5.498200425 5.4988003 5.499400225 5.5000002 5.500600225]
plot(x,y1,x,y2,x,y3)

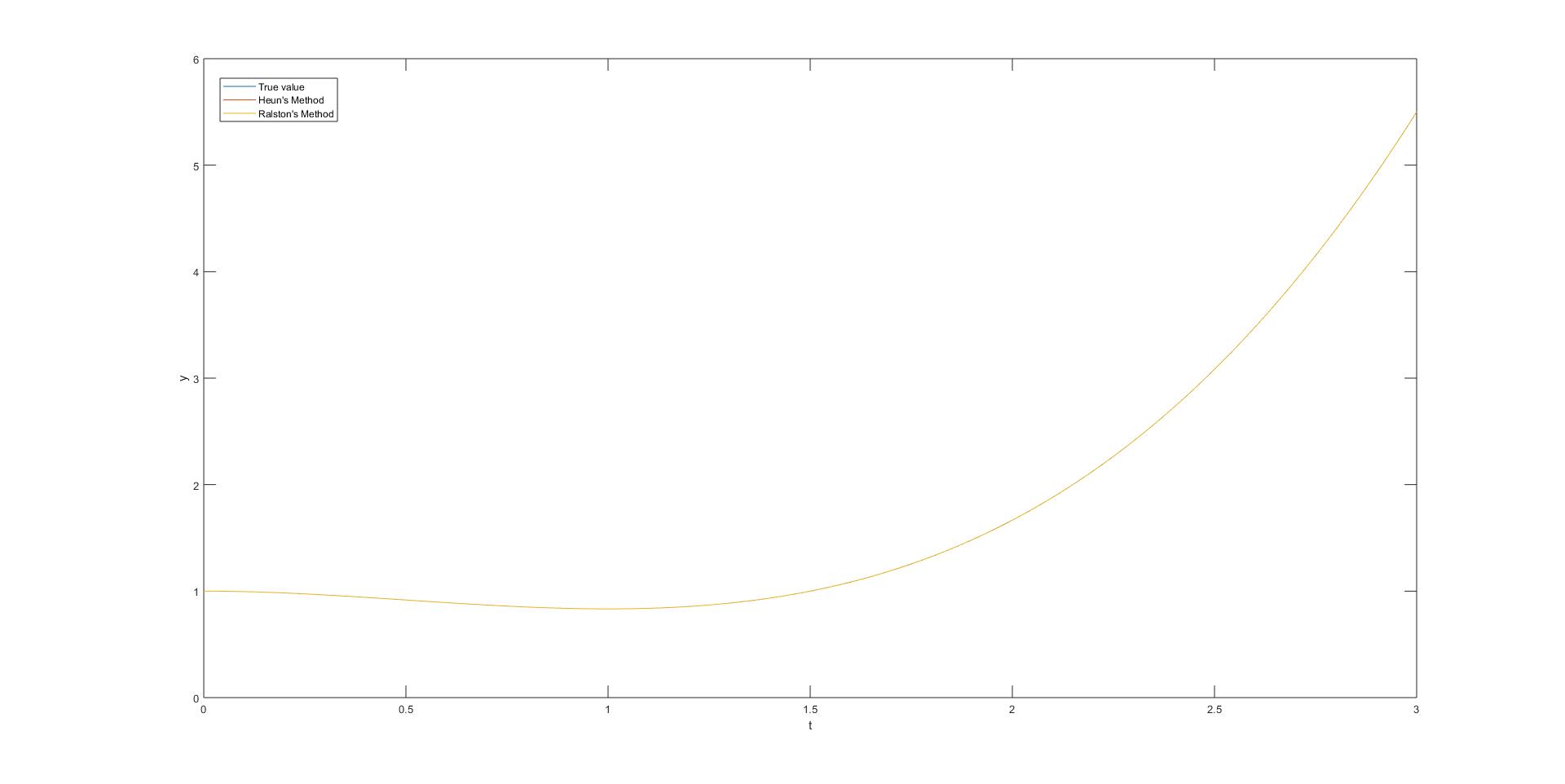
result-3

Conclusion

결론을 짓기 위해 h를 0.0001로 설정한 뒤 같은 코드를 살짝 수정해서 돌려보니 아래 그림과 같이 세 곡선이 모두 일정하게 그려졌다. 따라서 오차는 h값이 커서 났던 것이고 Ralston’s Method가 상대적으로 Heun’s Method보다 정확하다고 할 수 있다.