Numerical Analysis (4)

Posted on In

Least squares regression for a straight line

Process

  • Residual의 합 Sr을 구하여 미분
  • 각각의 Parameter에 대한 편미분 값이 0이 되도록 계산
  • 구한 a(0)와 a(1)의 값으로 식 구하기
  • The standard error of the estimate - S(y/x)
  • The correlation coefficient - r
  • (5, 5)라는 Data point가 주어질때, 유효한가?

원래의 Data point를 이용한 Regression

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
import math
import plotly
from plotly.graph_objs import Scatter, Layout


def sigma(a): #Defining sigma
    sum = 0
    for b in range(0, len(a)):
        sum = sum + a[b]
    return sum

def doublesigma(a, c): #Defining doublesigma
    sum = 0
    for b in range(0, len(a)):
        sum = sum + a[b] * c[b]
    return sum

def squaresigma(a): #Defining squaresigma
    sum = 0
    for b in range(0, len(a)):
        sum = sum + a[b]**2
    return sum

def reg(var): #Defining regression function
    return a0 + a1 * x[var]

def Sr(): #Defining deviation of residual Sr
    sum = 0
    for b in range(0, len(y)):
        sum = sum + (y[b] - reg(b))**2
    return sum

def St(): #Defining deviation of measurement St
    sum = 0
    for b in range(0, len(y)):
        sum = sum + (y[b] - sigma(y) / len(y))**2
    return sum

x = [5, 6, 10, 14, 16, 20, 22, 28, 28, 36, 38] #Defining data point of x
y = [30, 22, 28, 14, 22, 16, 8, 8, 14, 0, 4] #Defineing data point of y

a1 = (len(x) * doublesigma(x, y) - sigma(x) * sigma(y)) / (len(x) * squaresigma(x) - sigma(x)**2) #Determining a1
a0 = sigma(y) / len(y) - a1 * sigma(x) / len(x) #Determining a0
Sr = Sr()
St = St()
Syunderx = math.sqrt(Sr / (len(x)-2)) #Determining The standard error of the estimate S(y/x)
r = (len(x) * doublesigma(x, y) - sigma(x) * sigma(y)) / (math.sqrt(len(x) * squaresigma(x) - sigma(x)**2) * math.sqrt(len(y) * squaresigma(y) - sigma(y)**2)) #Determining The correlation coefficient r
print("a0 = %f, a1 = %f" %(a0, a1))
print("Sr = %f" %Sr)
print("Syunderx = %f" %Syunderx)
print("St = %f" %St)
print("r = %f" %abs(r))
print("r = %f" %math.sqrt((St - Sr) / St))

plotly.offline.plot({ #Data ploting
    "data": [Scatter(x=x, y=y)],
    "layout": Layout(title="Data point")
})

실행결과

1
2
3
4
5
6
7
8
9
"C:\Users\s_oh3417\PycharmProjects\수치 Proj3\venv\Scripts\python.exe" "C:/Users/s_oh3417/PycharmProjects/수치 Proj3/Main.py"
a0 = 30.739629, a1 = -0.771910
Sr = 173.735806
Syunderx = 4.393629
St = 938.909091
r = 0.902751
r = 0.902751

Process finished with exit code 0

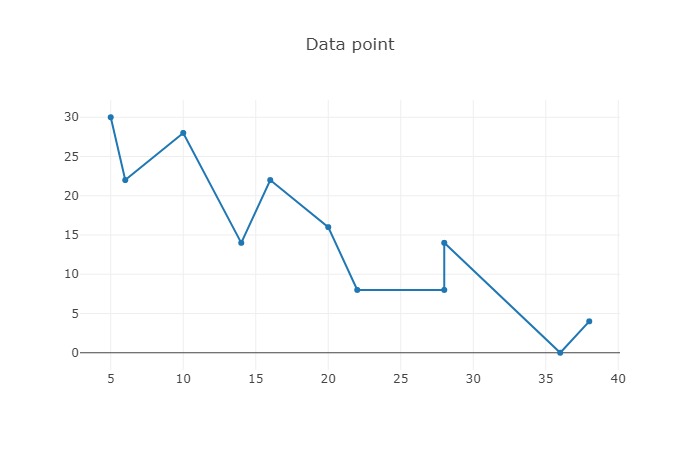
data-point
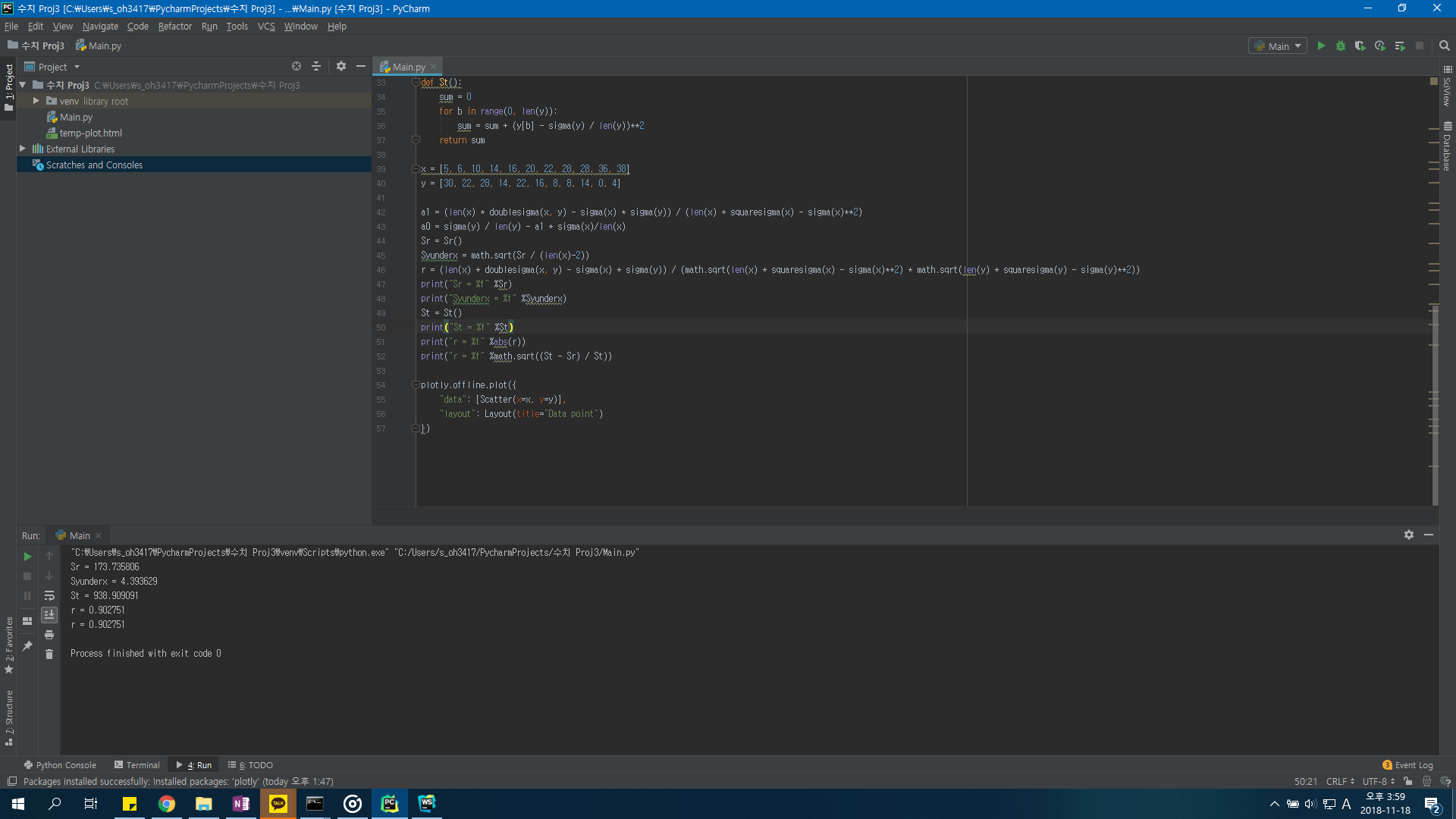
results
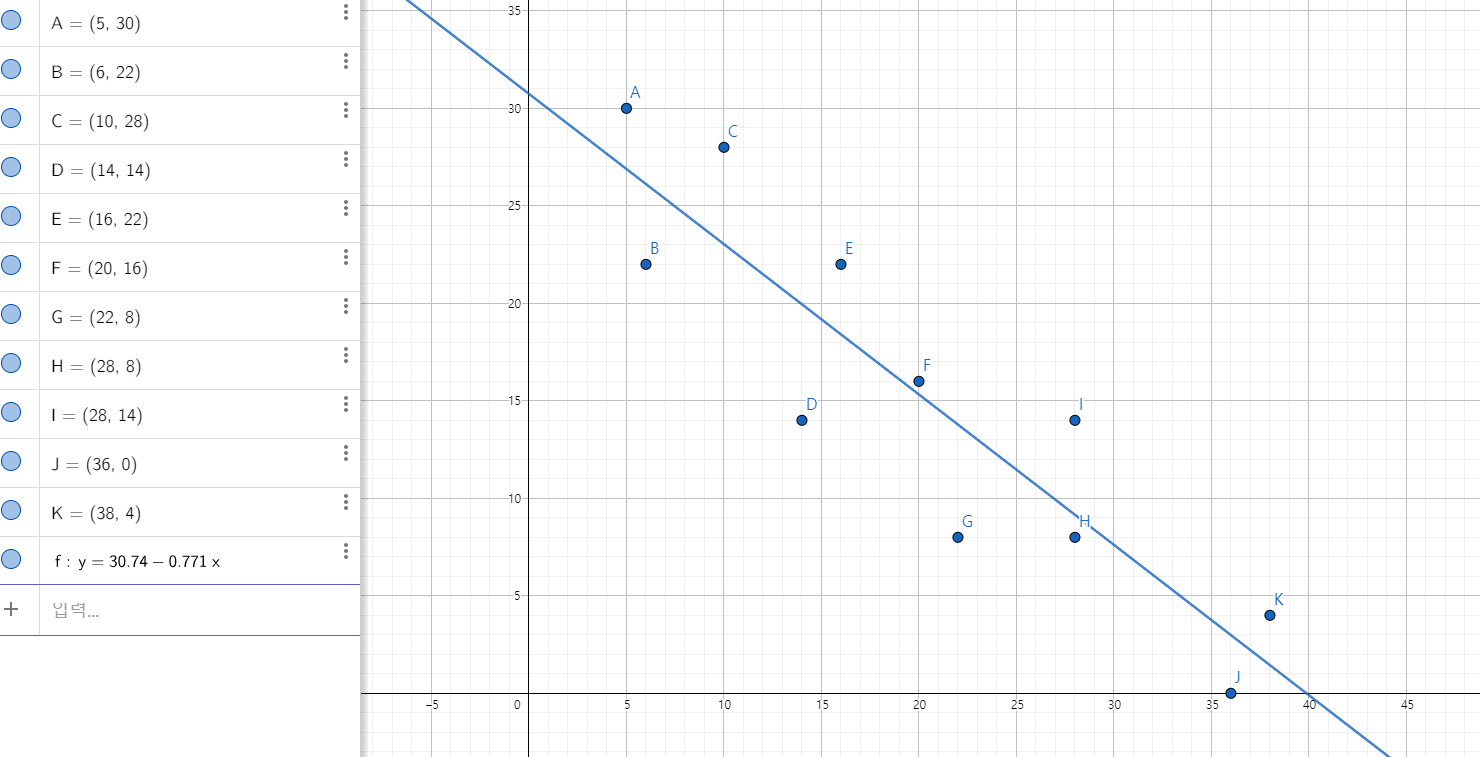
regression

(5, 5) Data point 추가한 Regression

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
import math
import plotly
from plotly.graph_objs import Scatter, Layout


def sigma(a): #Defining sigma
    sum = 0
    for b in range(0, len(a)):
        sum = sum + a[b]
    return sum

def doublesigma(a, c): #Defining doublesigma
    sum = 0
    for b in range(0, len(a)):
        sum = sum + a[b] * c[b]
    return sum

def squaresigma(a): #Defining squaresigma
    sum = 0
    for b in range(0, len(a)):
        sum = sum + a[b]**2
    return sum

def reg(var): #Defining regression function
    return a0 + a1 * x[var]

def Sr(): #Defining deviation of residual Sr
    sum = 0
    for b in range(0, len(y)):
        sum = sum + (y[b] - reg(b))**2
    return sum

def St(): #Defining deviation of measurement St
    sum = 0
    for b in range(0, len(y)):
        sum = sum + (y[b] - sigma(y) / len(y))**2
    return sum

x = [5, 6, 10, 14, 16, 20, 22, 28, 28, 36, 38, 5] #Defining data point of x
y = [30, 22, 28, 14, 22, 16, 8, 8, 14, 0, 4, 5] #Defineing data point of y

a1 = (len(x) * doublesigma(x, y) - sigma(x) * sigma(y)) / (len(x) * squaresigma(x) - sigma(x)**2) #Determining a1
a0 = sigma(y) / len(y) - a1 * sigma(x) / len(x) #Determining a0
Sr = Sr()
St = St()
Syunderx = math.sqrt(Sr / (len(x)-2)) #Determining The standard error of the estimate S(y/x)
r = (len(x) * doublesigma(x, y) - sigma(x) * sigma(y)) / (math.sqrt(len(x) * squaresigma(x) - sigma(x)**2) * math.sqrt(len(y) * squaresigma(y) - sigma(y)**2)) #Determining The correlation coefficient r
print("a0 = %f, a1 = %f" %(a0, a1))
print("Sr = %f" %Sr)
print("Syunderx = %f" %Syunderx)
print("St = %f" %St)
print("r = %f" %abs(r))
print("r = %f" %math.sqrt((St - Sr) / St))

plotly.offline.plot({ #Data ploting
    "data": [Scatter(x=x, y=y)],
    "layout": Layout(title="Data point")
})

실행결과

1
2
3
4
5
6
7
8
9
"C:\Users\s_oh3417\PycharmProjects\수치 Proj3\venv\Scripts\python.exe" "C:/Users/s_oh3417/PycharmProjects/수치 Proj3-1/Main.py"
a0 = 25.031041, a1 = -0.567423
Sr = 549.940254
Syunderx = 7.415796
St = 1032.250000
r = 0.683550
r = 0.683550

Process finished with exit code 0

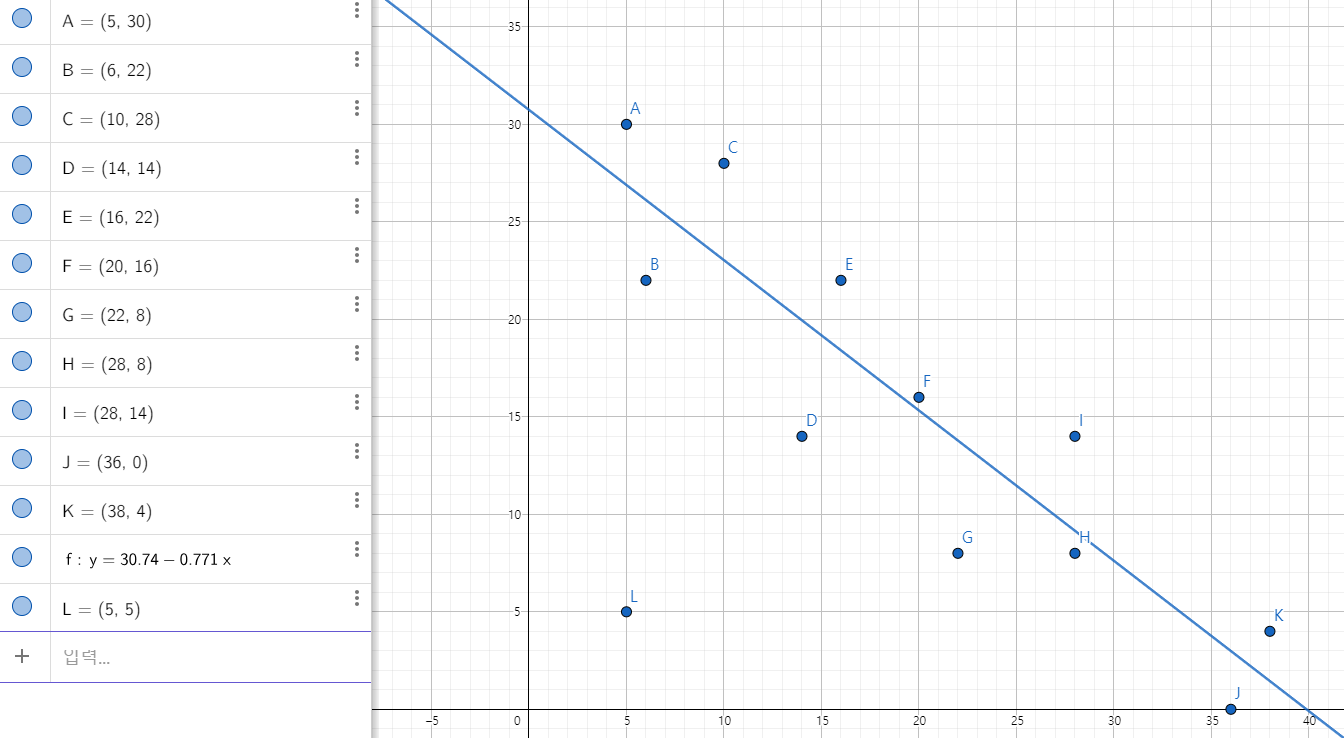
regression-1
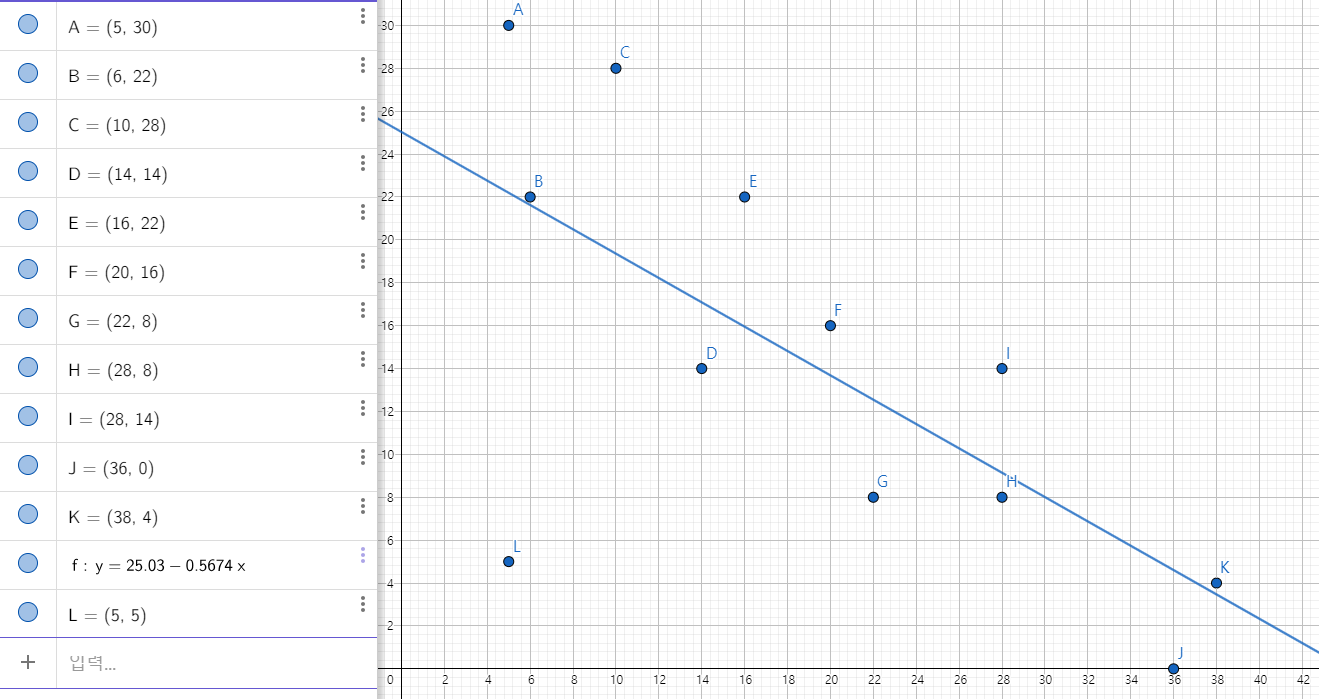
regression-2

Conclusion

따라서 (5, 5)는 Visual assessment로 적절치 않으며, Sr의 값이 3배 가량 증가했으므로 오류가 매우 커짐을 알 수 있으므로 유효하지 않다고 볼 수 있다