Numerical Analysis (3)

Posted on In

Newton-Raphson method

1
2
def newrap(x):
    return x - f(x) / f1(x)

Root for the algebraic equation using Newton-Raphson method

Process

  • N-R Method로 Numerical analysis
  • (a), (b)의 시작점으로 값을 찾는다
  • True relative error를 구한다
  • MATLAB으로 Plot
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def f(x): #f(x)
    return - 2 + 6 * x - 4 * x ** 2 + 0.5 * x ** 3


def f1(x): #f'(x)
    return 6 - 8 * x + 1.5 * x ** 2


def newrap(x): #Newton-Raphson method
    return x - f(x) / f1(x)


a = 4.43 # initial guess
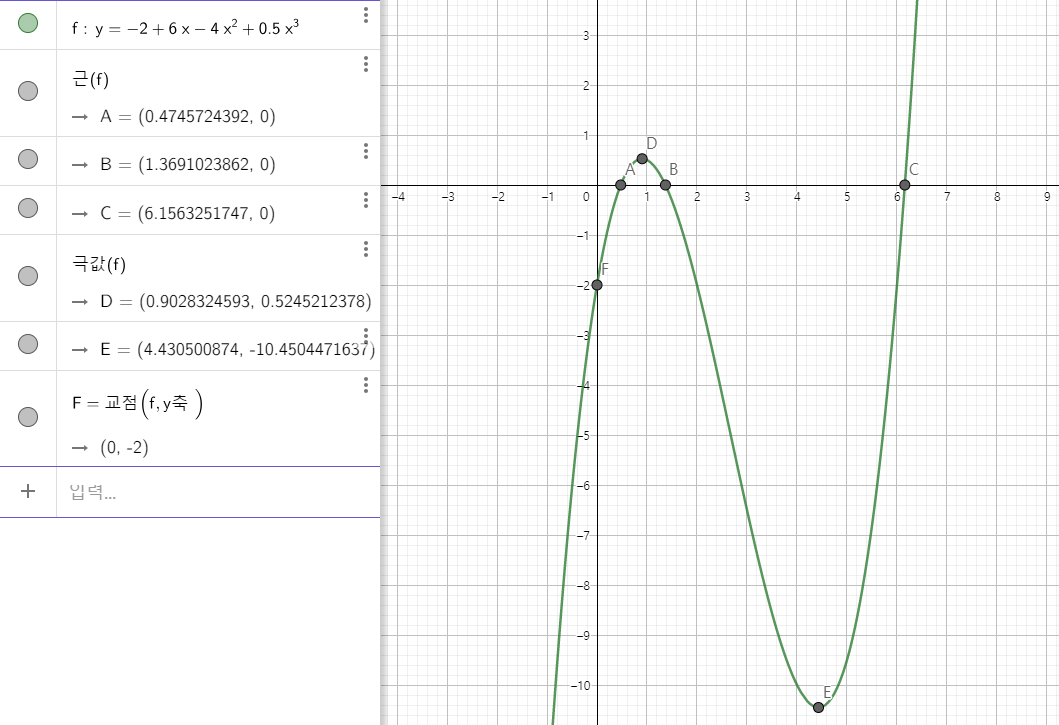
sol = 0.47457 #solution
lis = [] #solution in list

for z in range(0 ,30):
    a = round(a, 2) # round off
    esubt = abs(((a - sol) / sol) * 100) #True relative error
    esubt = round(esubt, 2) #round off
    a = newrap(a) #use N-R method
    lis = lis + [esubt]
    print(esubt)

print(lis)
1
2
3
4
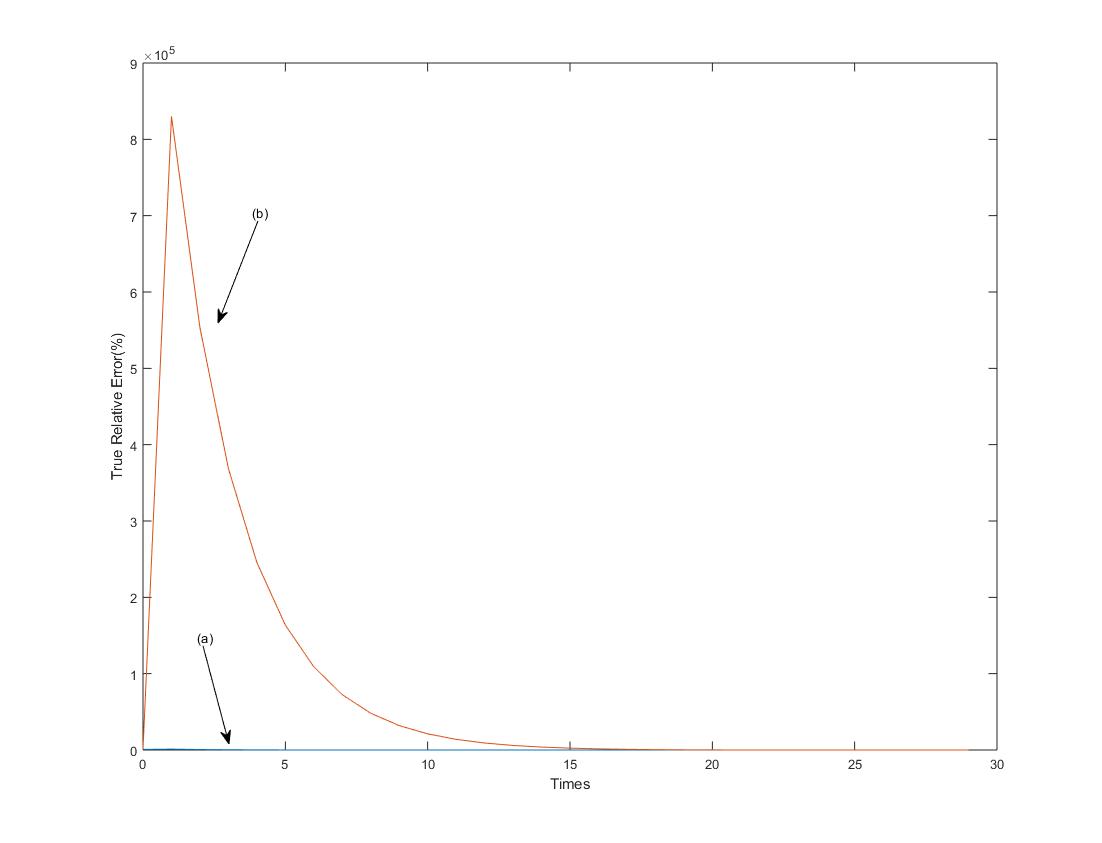
x = [0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29];
y = [785.01, 1121.98, 641.54, 340.22, 156.89, 57.86, 13.61, 0.96, 0.96, 0.96, 0.96, 0.96, 0.96, 0.96, 0.96, 0.96, 0.96, 0.96, 0.96, 0.96, 0.96, 0.96, 0.96, 0.96, 0.96, 0.96, 0.96, 0.96, 0.96, 0.96];
y2 = [833.48 830141.93 553274.45 368696.84 245644.39 163610.12 108920.62 72460.24 48154.03 31949.89 21148.53 13948.33 9150.3 5955.83 3829.69 2419.99 1488.63 879.65 487.72 245.39 104.21 32.57 5.18 0.96 0.96 0.96 0.96 0.96 0.96 0.96];
plot(x,y,x,y2)

Solution
실행결과