The Lateral Dynamics of a Moving Web

Posted on In

Introduction

사행이란 무엇인가…

John Jarvis Shelton

Sign Conventions for Mechanics Analysis.

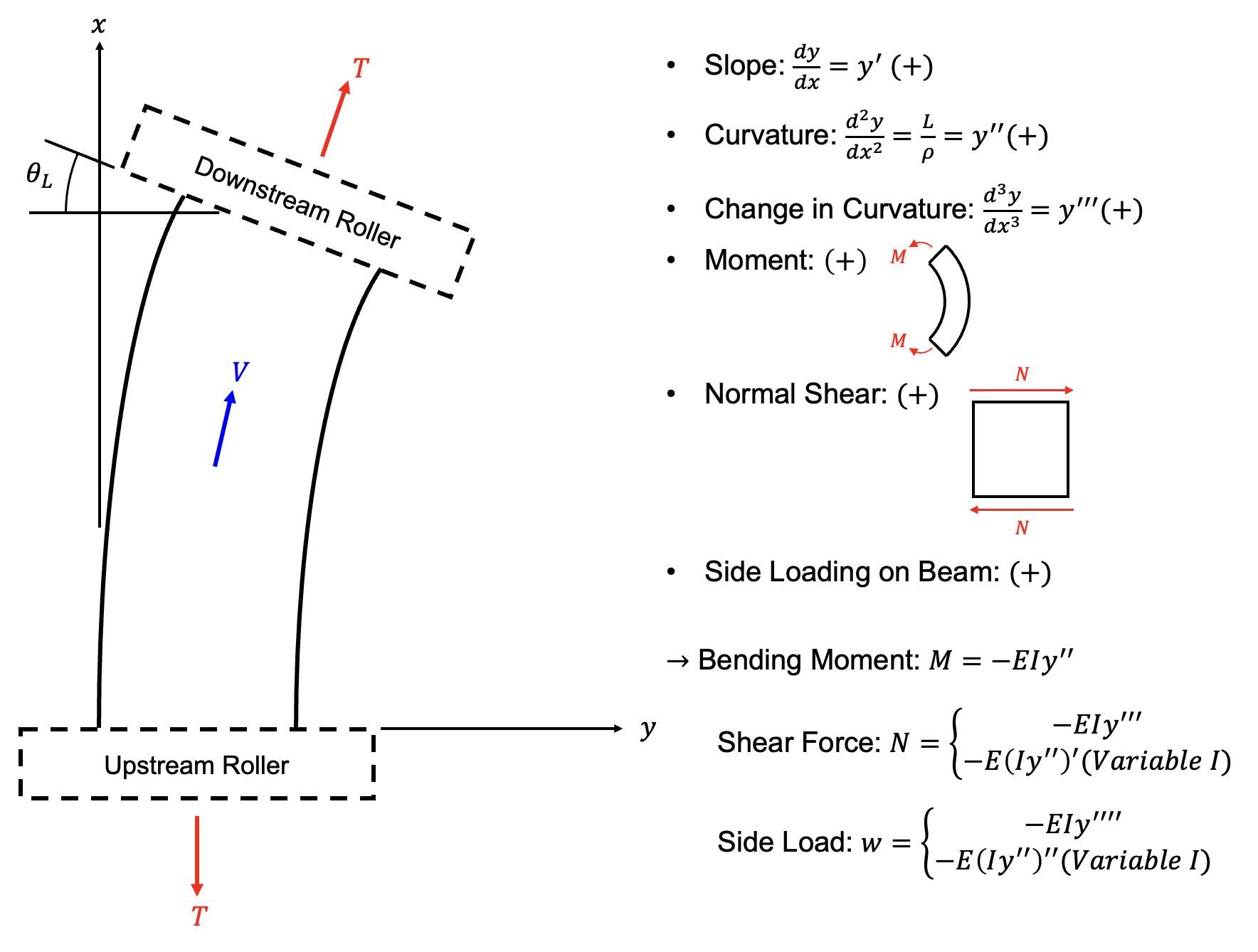
sign-conventions-for-mechanics-analysis.

Freebodies and Symbols for Steady-State Analysis.

freebodies-and-symbols-for-steady-state-analysis.
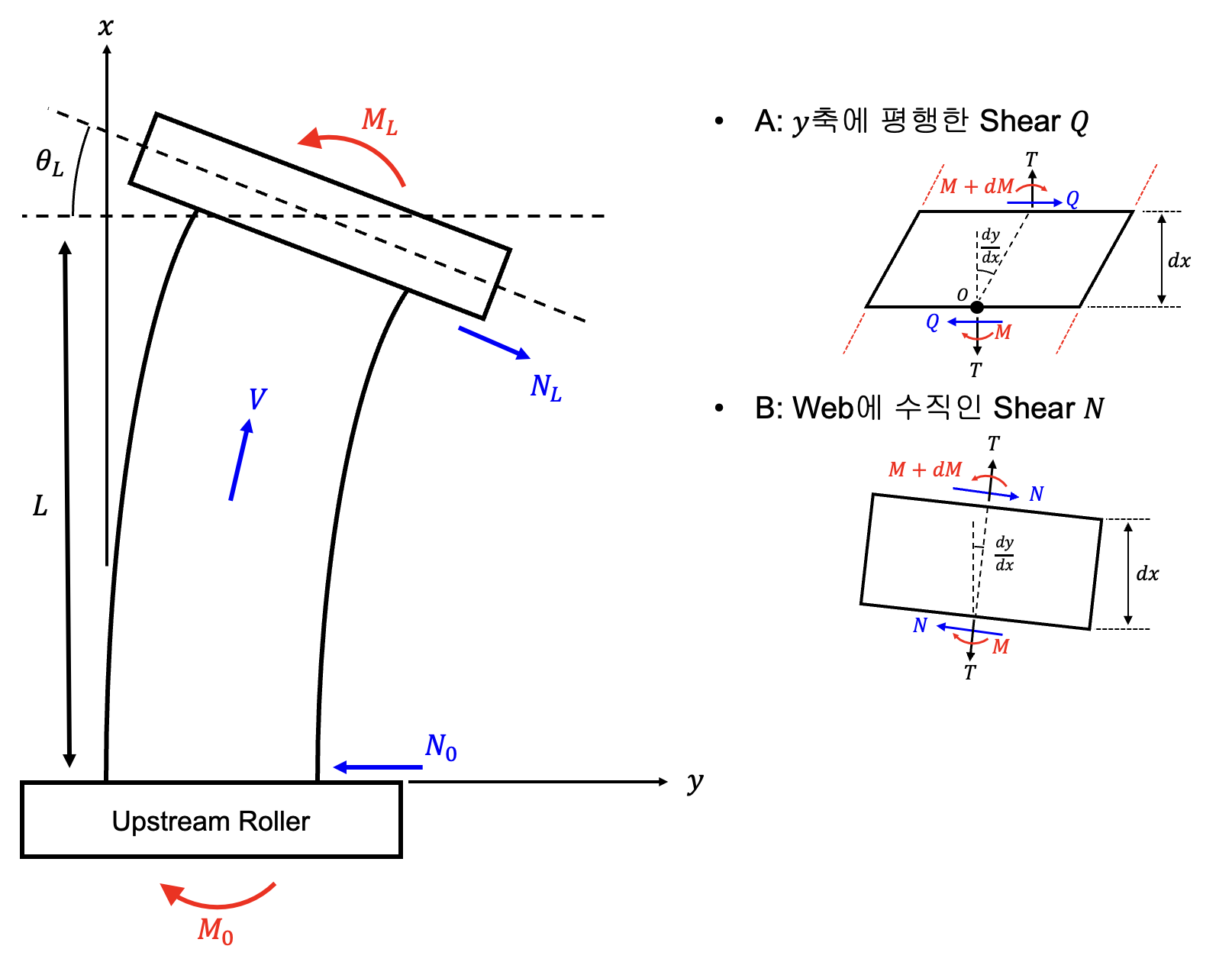
  • $Q$: Shear parallel to $y$ axis
  • $N$: Shear normal to web

If deflections are small, the tesnion $T$ of “A” and “B” are approximately equal.

  • “A”: Moment equilibrium at Point $O$

$$M+Qdx-(M+dM)-T\frac{dy}{dx}dx=0$$

$$Qdx-dM-Tdy=0$$

$$Q=\frac{dM}{dx}+T\frac{dy}{dx}$$

$$\frac{dM}{dx}=-EIy’’’(\because M=-EIy’’)$$

$$Q=-EIy’’’+T\frac{dy}{dx}$$

$$Q=Constant(\because Side\ load\ w = 0)\rightarrow -EIy’’’’+Ty’’=0$$

$$\therefore y’’’’-\frac{T}{EI}y’’=y’’’’-K^2y’’=0(K^2=\frac{T}{EI})$$

  • Beam Theory

$$
\frac{\partial^4y}{\partial x^4}-K^2\frac{\partial^2y}{\partial x^2}=0
$$
$$
N=Q-T\frac{dy}{dx}
$$

  • General Solution

$$
y(x)=C_1\sinh{Kx}+C_2\cosh{Kx}+C_3x+C_4
$$

Note that need 4 boundary conditions for this solution.

Static Model

  1. $y(0)=0\rightarrow C_2=-C_4$
  2. Upstream roller에서 web과 roller 사이의 마찰이 충분하여 circumferential slip과 lateral slip이 없다면 $y’(0)=0$을 만족한다.
    • Normal Entry Law: 기울기가 0이므로 web이 roller에 수직으로 입사
  3. At $x=L$ (No Slip Condition을 만족해야 Normal Entry Law 성립)
    • $y’(L)=C_1K\cosh{KL}+C_2K\sinh{KL}+C_3=\theta_L$

$$C_1K\cosh{KL}+C_2K\sinh{KL}-C_1K=\theta_L$$

$$C_2K\sinh{KL}=\theta_L-C_1K\cosh{KL}+C_1K$$

$$C_2=\frac{\theta}{K\sinh{KL}}-C_1\frac{\cosh{KL}-L}{\sinh{KL}}$$

Web With Moment at Guide Roller.

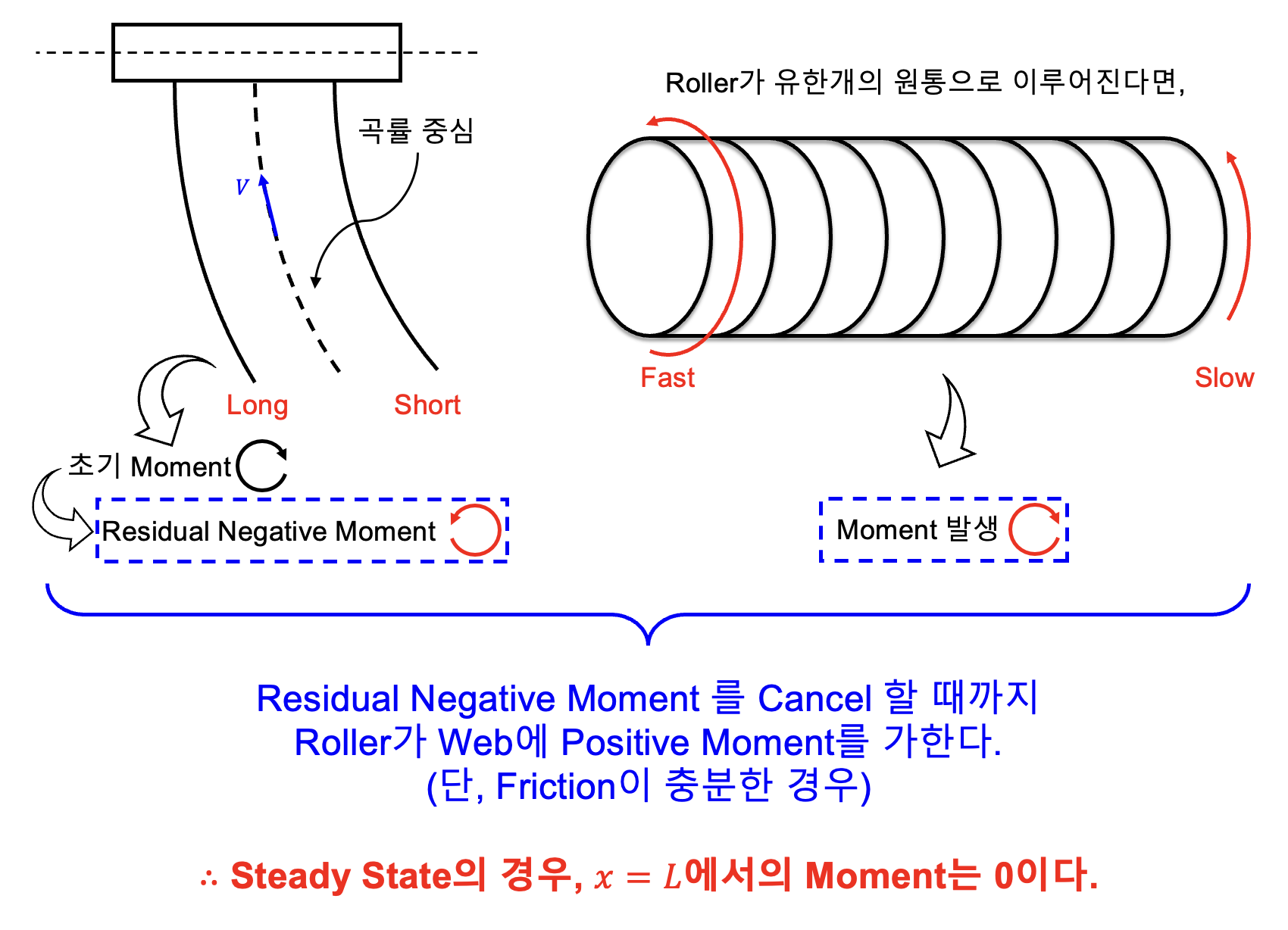
web-with-moment-at-guide-roller.
  1. At steady state, moment of guider roll is zero.

$$M_L=-EIy’’=0\rightarrow y’’(L)=0$$

$$y’’(x)=K^2C_1\sinh{Kx}+K^2C_2\cosh{Kx}$$

$$y’’(L)=0\rightarrow K^2C_1\sinh{KL}+K^2C_2\cosh{KL}=0$$

$$\therefore C_2=-C_1\frac{\sinh{KL}}{\cosh{KL}}$$

  1. $C_2=\frac{\theta_L}{K\sinh{KL}}-C_1\frac{\cosh{KL}-1}{\sinh{KL}}(\because 3.)$, $C_2=-C_1\frac{\sinh{KL}}{\cosh{KL}}(\because 4.)$

$$
\frac{\theta_L}{K\sinh{KL}}-C_1\frac{\cosh{KL}-1}{\sinh{KL}}=-C_1\frac{\sinh{KL}}{\cosh{KL}}
$$

$$
\theta_L=C_1\frac{(\cosh{KL})^2-\cosh{KL}-(\sinh{KL})^2}{\cosh{KL}\times\sinh{KL}}\times K\sinh{KL}
$$

$$
\therefore C_1=-\frac{\theta_L}{K}\times\frac{\cosh{KL}}{\cosh{KL}-1}
$$

$$
C_2=-C_1\frac{\sinh{KL}}{\cosh{KL}}=\frac{\theta_L}{K}\times\frac{\cosh{KL}}{\cosh{KL}-1}\times\frac{\sinh{KL}}{\cosh{KL}}=\frac{\theta_L}{K}\times\frac{\sinh{KL}}{\cosh{KL}-1}
$$

$$
C_3=-KC_1=\theta_L\frac{\cosh{KL}}{\cosh{KL}-1}
$$

$$
C_4=-C_2=-\frac{\theta_L}{K}\times\frac{\sinh{KL}}{\cosh{KL}-1}
$$

  • Particular Solution

$$
y(x)=-\frac{\theta_L}{K}\times\frac{\cosh{KL}}{\cosh{KL}-1}\sinh{Kx}+\frac{\theta_L}{K}\times\frac{\sinh{KL}}{\cosh{KL}-1}\cosh{Kx}
+\theta_L\frac{\cosh{KL}}{\cosh{KL}-1}x-\frac{\theta_L}{K}\times\frac{\sinh{KL}}{\cosh{KL}-1}
$$

  1. Non-dimensionalized by dividing by $L$

$$
\begin{aligned}
\frac{y}{L}&=\theta_L[-\frac{1}{KL}\frac{\cosh{KL}}{\cosh{KL}-1}\sinh{Kx}\newline
&+\frac{1}{KL}\frac{\sinh{KL}}{\cosh{KL}-1}\cosh{Kx}+\frac{x}{L}\frac{\cosh{KL}}{\cosh{KL}-1}-\frac{1}{KL}\frac{\sinh{KL}}{\cosh{KL}-1}]
\end{aligned}
$$

$$
\frac{y}{L}=\theta_L[\frac{\cosh{KL}}{\cosh{KL}-1}(\frac{x}{L}-\frac{\sinh{Kx}}{KL})+\frac{1}{KL}\frac{\sinh{KL}}{\cosh{KL}-1}(\cosh{Kx}-1)]
$$

  1. Let curvature factor $K_c=\frac{y_L}{L\theta_L}$

$$
\begin{aligned}
K_c&=\frac{\cosh{KL}}{\cosh{KL}-1}(1-\frac{\sinh{KL}}{KL})+\frac{1}{KL}\frac{\sinh{KL}}{\cosh{KL}-1}(\cosh{KL}-1)\newline
\newline
&=\frac{KL\cosh{KL}-(\cosh{KL})(\sinh{KL})+(\sinh{KL})(\cosh{KL})-\sinh{KL}}{KL(\cosh{KL}-1)}
\end{aligned}
$$

$$
\therefore Curvature\ factor:\ K_c=\frac{KL\cosh{KL}-\sinh{KL}}{KL(\cosh{KL}-1)}
$$

$$ \lim_{KL\rightarrow0}K_c=\frac{2}{3} $$
  • Lateral web deflection from it’s original position

$$
y(x)=\theta_L[\frac{\cosh{KL}}{\cosh{KL}-1}(x-\frac{\sinh{Kx}}{K})+\frac{1}{K}\frac{\sinh{KL}}{\cosh{KL}-1}(\cosh{Kx}-1)]
$$

  • Angle between web and roller

$$
\frac{dy}{dx}=\theta(x)=\theta_L[\frac{\cosh{KL}}{\cosh{KL}-1}(1-\cosh{KL})+\frac{\sinh{KL}}{\cosh{KL}-1}\sinh{Kx}]
$$

$$
y’’=\frac{d^2y}{dx^2}=\theta_L[-\frac{K\cosh{KL}}{\cosh{KL}-1}\sinh{Kx}+\frac{K\sinh{KL}}{\cosh{KL}-1}\cosh{Kx}]
$$

  1. $EIK^2=T$이므로 $EIK=\frac{T}{K}$
  • Bending moment in the web

$$
\begin{aligned}
M(x)=-EIy’’&=\theta_L[EIK\frac{\cosh{KL}}{\cosh{KL}-1}\sinh{Kx}-EIK\frac{\sinh{KL}}{\cosh{KL}-1}\cosh{Kx}]\newline
&=-\frac{T}{K}\theta_L[\frac{\sinh{KL}}{\cosh{KL}-1}\cosh{Kx}-\frac{\cosh{KL}}{\cosh{KL}-1}\sinh{Kx}]
\end{aligned}
$$

$$
y’’’=\frac{d^3y}{dx^3}=\theta_L[-\frac{K^2\cosh{KL}}{\cosh{KL}-1}\cosh{Kx}+\frac{K^2\sinh{KL}}{\cosh{KL}-1}\sinh{Kx}]
$$

  • Shear force normal to the elastic curve of the web

$$
N(x)=-EIy’’’=T\theta_L[\frac{\cosh{KL}}{\cosh{KL}-1}\cosh{Kx}-\frac{\sinh{KL}}{\cosh{KL}-1}\sinh{Kx}]
$$

Critical Moment Condition

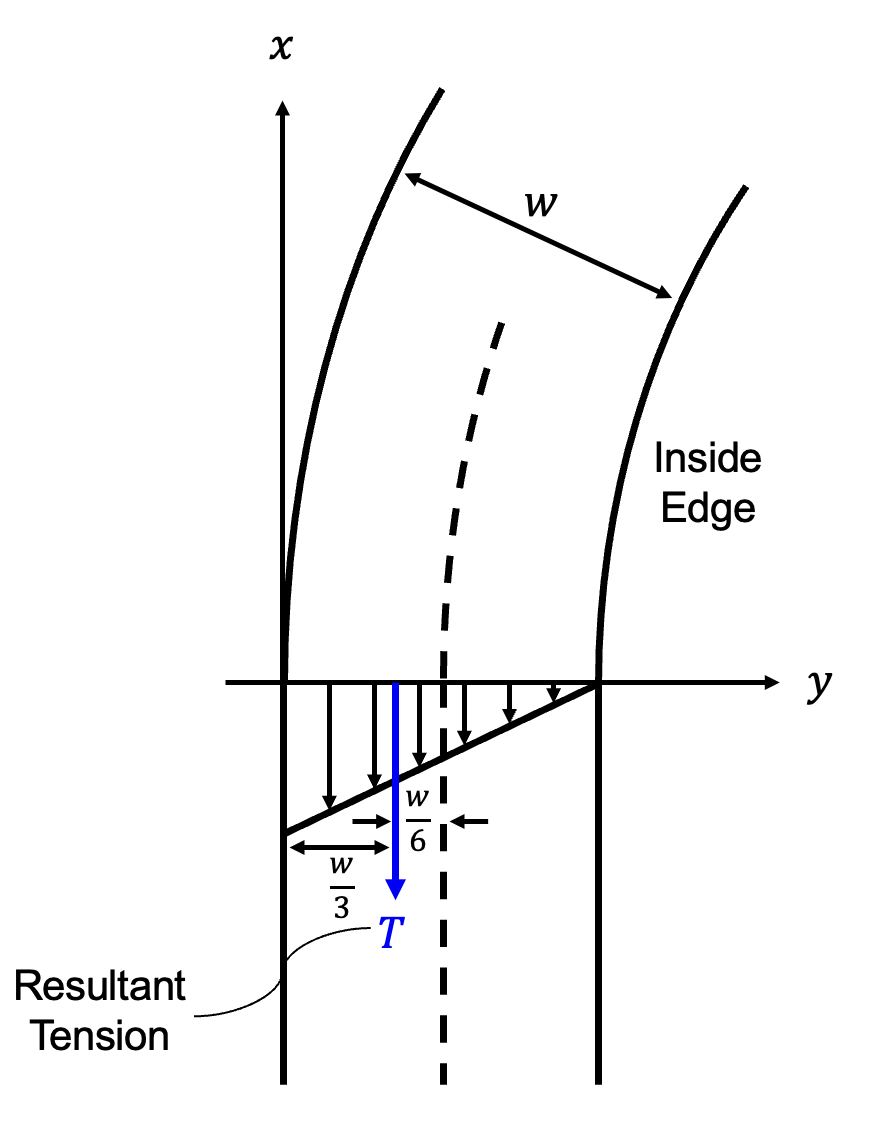
critical-moment-condition
  1. Maximum moment occurs at $x=0$ (Upstream roller)

$$
M_0=\frac{-\sinh{KL}}{\cosh{KL}-1}\frac{T}{K}\theta_L
$$

Inside edge에서 $x=0$인 점의 resultant tension을 0으로 만드는 condition을 critical condition이라면,

$$
(M_0)_{cr}=-\frac{Tw}{6}=-\frac{\sinh{KL}}{\cosh{KL}-1}\frac{T}{K}(\theta_L)_{cr}
$$

$$
(\theta_0)_{cr}=\frac{KL}{6}\frac{w}{L}\frac{\cosh{KL}-1}{\sinh{KL}}
$$

Downstream roll이 $(\theta_L)_{cr}$만큼의 각도를 가지면 $x=0$에서부터 bending 발생

  • Slack이 발생하지 않는 최대 수정량 (Guide)

$$
\begin{aligned}
(\frac{y_L}{w})_{cr}&=\frac{KL}{6}K_c\frac{\cosh{KL}-1}{\sinh{KL}}\newline
&=\frac{1}{6}\frac{KL\cosh{KL}-\sinh{KL}}{\sinh{KL}}(\because y_L=K_c\theta_LL)
\end{aligned}
$$

Upstream Roller에 $\theta_0$의 각도가 존재하는 Case

$$ y(0)=0,\ y'(0)=\theta_0,\ y'(L)=\theta_L,\ y''(0)=0 $$

$$
\begin{aligned}
\frac{y}{L}&=\theta_L(1-\frac{\theta_0}{\theta_L})[\frac{\cosh{KL}}{\cosh{KL}-1}(\frac{x}{L}-\frac{\sinh{Kx}}{KL})\newline
&+\frac{1}{KL}\frac{\sinh{KL}}{\cosh{KL}-1}(\cosh{Kx}-1)]+(\frac{x}{L})\theta_0
\end{aligned}
$$

$$
\frac{y_L}{L\theta_L}=(1-\frac{\theta_0}{\theta_L})[\frac{KL\cosh{KL}-\sinh{KL}}{KL(\cosh{KL}-1)}]+\frac{\theta_0}{\theta_L}
$$

  • Angle between web and roller
$$ \begin{aligned} \frac{dy}{dx}=\theta(x)=&\theta_L(1-\frac{\theta_0}{\theta_L})[\frac{\cosh{KL}}{\cosh{KL}-1}(1-\cosh{Kx})\newline &+\frac{\sinh{KL}}{\cosh{KL}-1}\sinh{Kx}]+\theta_0 \end{aligned} $$
  • Bending moment in the web

$$
M(x)=\frac{T}{K}(1-\frac{\theta_0}{\theta_L})\theta_L[\frac{\cosh{KL}}{\cosh{KL}-1}(\sinh{Kx})-\frac{\sinh{KL}}{\cosh{KL}-1}\cosh{Kx}]
$$

  • Shear force normal to the elastic curve of the web

$$
N(x)=T\theta_L(1-\frac{\theta_0}{\theta_L})[\frac{\cosh{KL}}{\cosh{KL}-1}(\cosh{Kx})-\frac{\sinh{KL}}{\cosh{KL}-1}\sinh{Kx}]
$$

  • Critical condition인 경우 maximum moment $M_0$ (at $x=0$)

$$
M_0=-\frac{\sinh{KL}}{\cosh{KL}-1}(\frac{T}{K}\theta_L)(1-\frac{\theta_0}{\theta_L})
$$

  • Critical guide roller angle

$$
(\theta_L)_{cr}=\frac{KL}{6}\frac{w}{L}\frac{\cosh{KL}-1}{\sinh{KL}}+\theta_0
$$

  • Critical correction

$$
(\frac{y_L}{w})_{cr}=\frac{1}{6}\frac{KL\cosh{KL}-\sinh{KL}}{\sinh{KL}}+\frac{L}{w}\theta_0
$$