Hands-on Machine Learning (3)

Posted on In

Ensemble Learning and Random Forests

  • Ensemble learning: 일련의 예측기 (ensemble)로부터 예측 수집
    • 가장 좋은 모델 하나보다 더 좋은 예측 취득 가능
    • Ensemble method: 앙상블 학습 알고리즘
  • Random forest: 결정 트리의 앙상블
    • 훈련 세트로부터 무작위로 각기 다른 서브셋을 만들고 일련의 결정 트리 분류기 훈련
    • 모든 개별 트리의 예측 중 가장 많은 선택을 받은 클래스를 예측으로 선정

Voting Classifiers

  • Hard voting (직접 투표): 각 분류기의 예측을 모아 가장 많이 선택된 클래스 예측
    • 큰 수의 법칙 (law of large numbers)에 의해 앙상블에 포함된 개별 분류기 중 가장 뛰어난 것보다 다수결 투표 분류기의 정확도가 보통 더 높음
  • Soft voting (간접 투표): 각 분류기의 예측 확률을 평균 내어 가장 높은 확률인 클래스 예측
    • 모든 분류기가 클래스의 확률을 예측할 수 있어야함 (probability = True)

Individual classifiers vs. voting classifier
individual-classifiers-vs.-voting-classifier

Bagging and Pasting

  • 같은 알고리즘 사용, 훈련 세트의 서브셋을 무작위로 구성 및 훈련
    • Bagging (bootstrap aggregating): 훈련 세트에서 중복을 허용하여 샘플링
    • Pasting: 훈련 세트에서 중복을 허용하지 않고 샘플링
  • 모든 예측기가 훈련을 마치면 예측을 수집하여 새로운 샘플에 대한 예측 생성
    • 수집 함수
      • Classification: 통계적 최빈값 (statistical mode)
      • Regression: 평균 (average)
    • 개별 예측기는 원본 훈련 세트로 훈련시킨 것보다 편향되어 있지만 수집 함수를 통해 편향과 분산 감소
    • 일반적으로 앙상블의 결과는 원본 데이터셋으로 하나의 예측기를 훈련시킬 때와 비교하여 편향은 비슷하지만 분산 감소
  • BaggingClassifier, BaggingRegressor
    • bootstrap = True: Bagging
    • bootstrap = False: Pasting
    • n_jobs: 훈련과 예측에 사용할 CPU 코어 수 (-1 지정 시 모든 가용 코어 사용)
1
2
3
4
5
6
7
8
tree_clf = DecisionTreeClassifier(random_state=42)
tree_clf.fit(X_train, y_train)

bag_clf = BaggingClassifier(
    DecisionTreeClassifier(), n_estimators = 500,
    max_samples = 100, bootstrap = True, n_jobs = -1
)
bag_clf.fit(X_train, y_train)

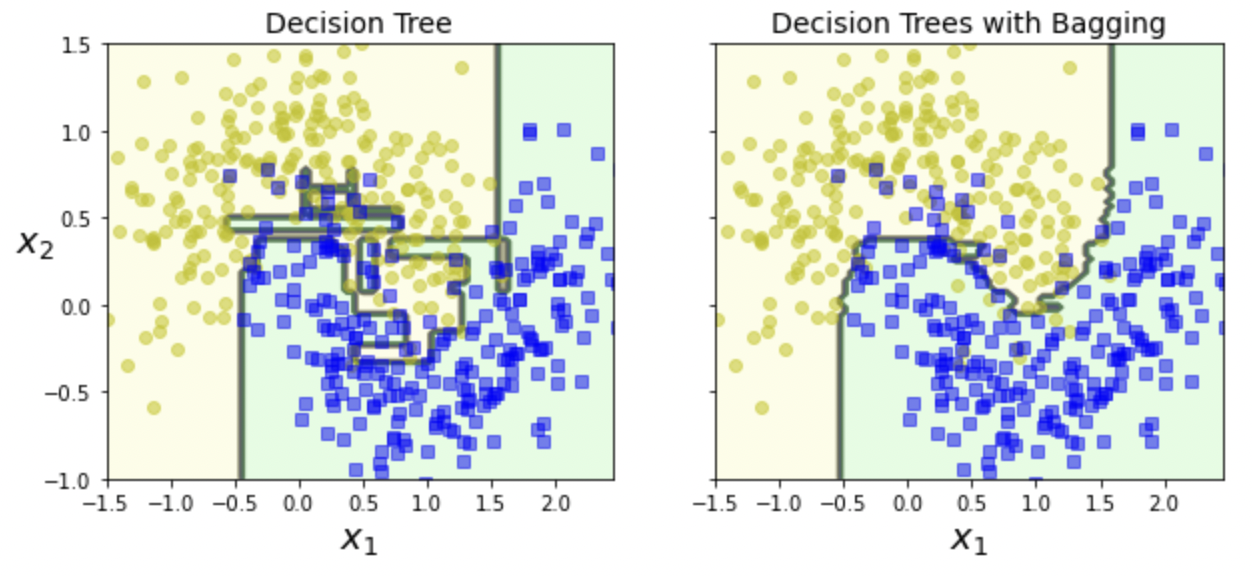
Decision tree vs. Decision trees with bagging
decision-tree-vs.-decision-trees-with-bagging

  • oob (out-of-bag) sample: 선택되지 않은 훈련 샘플의 나머지 37%를 의미
    • BaggingClassifier(bootstrap = True)
      • 중복을 허용하고 훈련 세트의 크기만큼인 m개의 샘플 선택
      • 평균적으로 각 예측기에 훈련 샘플의 63%만 샘플링
    • 앙상블의 평가: 각 예측기의 oob 평가 후 평균값 이용 $\rightarrow$ bag_clf.oob_score_
      • oob_score = True 필요
      • 예측기가 훈련되는 동안에는 oob sample을 사용하지 않으므로 별도의 검증 세트를 사용하지 않고 oob sample 사용

oob vs. accuracy
oob-vs.-accuracy

Random Patches and Random Subspaces

  • BaggingClassifier의 특성 샘플링: max_features, bootstrap_features를 통해 샘플링 조절
    • 무작위로 선택한 입력 특성의 일부분으로 각 예측기 훈련
    • 고차원 데이터셋을 다룰 때 유용
    • 더 다양한 예측기를 생성하여 편향을 늘리는 대신 분산 감소
  • Random patches method: 훈련 특성과 샘플을 모두 샘플링
  • Random subspaces method
    • 훈련 샘플 모두 사용: bootstrap = False, max_samples = 1.0
    • 특성 샘플링: bootstrap_features = True, max_features <= 1.0

Random Forest

  • Random forest: 배깅 혹은 페이스팅을 적용한 결정 트리의 앙상블
    • max_samples: 훈련 세트의 크기 지정
    • RandomForestClassifier, RandomForestRegressor 사용

Random forest
random-forest

  • Extremely randomized trees (extra-trees): 극단적으로 무작위한 트리의 랜덤 포레스트
    • 트리의 노드: 무작위 특성의 서브셋을 만들어 분할에 사용
    • 트리를 더욱 무작위하게 만들기 위해 최적의 임계값 대신 후보 특성을 사용해 무작위로 분할 후 최상의 분할 선택
    • 편향이 증가하지만 분산 감소
    • ExtraTreesClassifier, ExtraTreesRegressor 사용
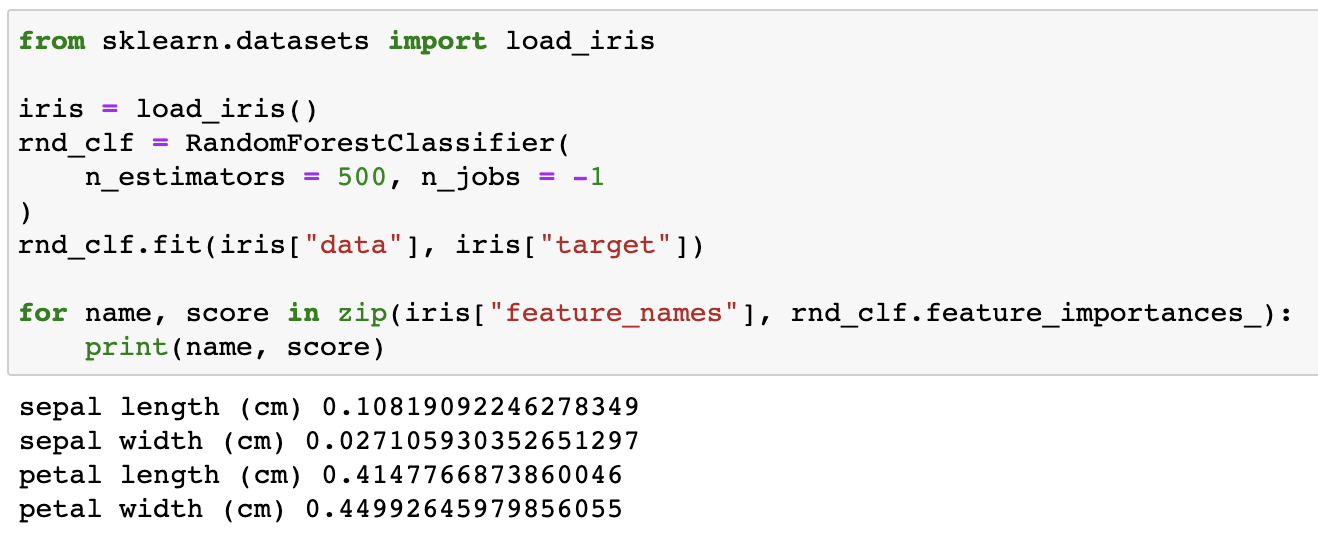
  • Feature importance: 랜덤 포레스트를 통해 특성의 상대 중요도 측정
    • 어떤 특성을 사용한 노드가 평균적으로 불순도를 얼마나 감소시키는지 정량적 평가
    • 가중치 평균 (각 노드의 가중치는 연관된 훈련 샘플 수와 동일)
    • feature_importances_ 사용

Feature importance
feature-importance

Boosting

  • Boosting (hypothesis boosting): 약한 학습기 다수를 연결하여 강한 학습기를 생성하는 앙상블 방법
    • AdaBoost (adaptive boosting): 이전 모델이 과소적합했던 훈련 샘플의 가중치를 높혀 학습하기 어려운 샘플 훈련
      1. 첫 번째 분류기를 훈련 세트에서 훈련 및 예측
      2. 훈련된 분류기가 잘못 분류한 샘플의 가중치 증가
      3. 두 번째 분류기는 업데이트된 가중치가 적용된 훈련 세트로 훈련
      4. 반복…
      • AdaBoostClassifier, AdaBoostRegressor 사용
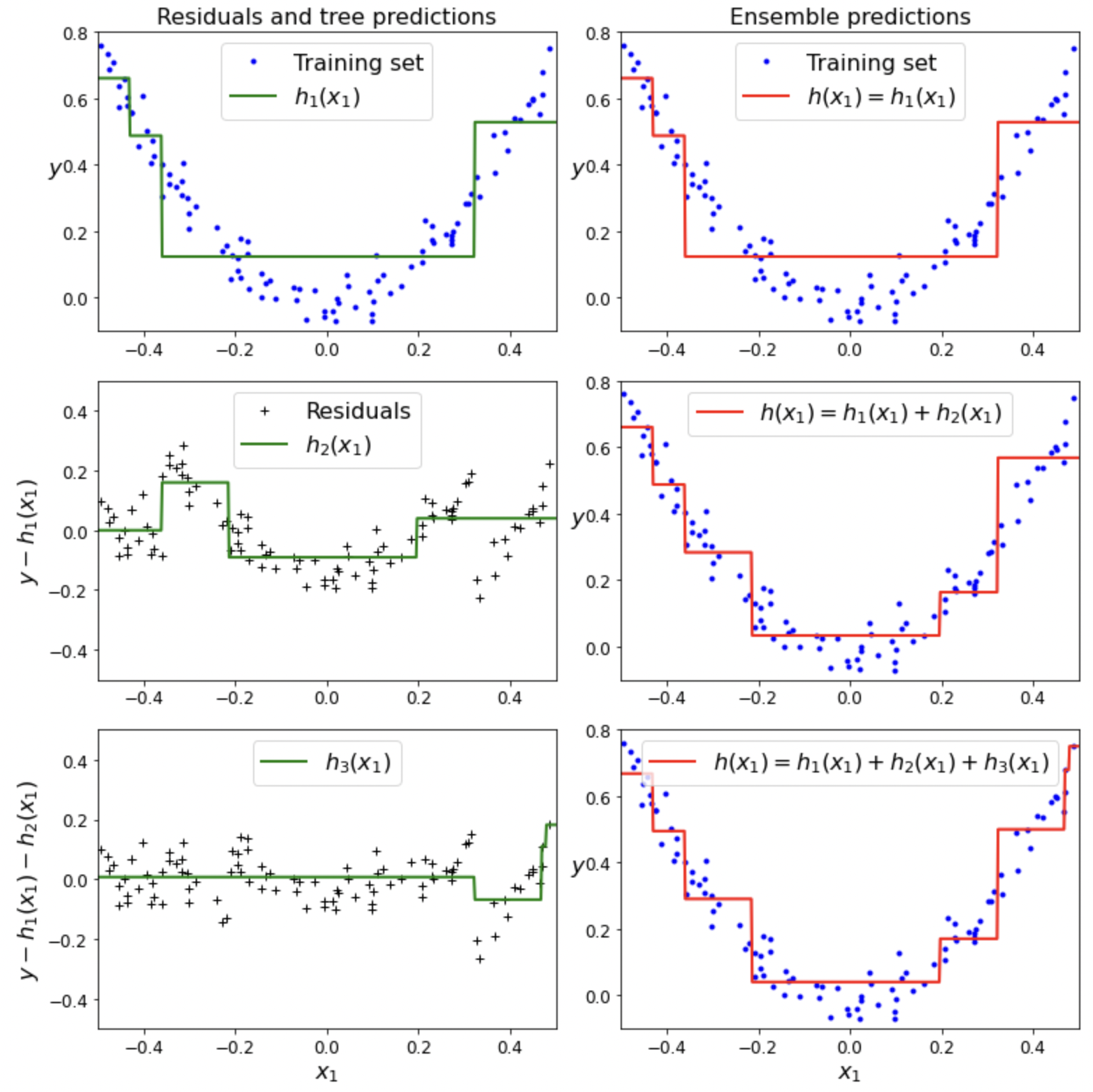
    • Gradient boosting: 예측기가 생성한 잔여 오차 (residual error)에 새로운 예측기 학습
      • Gradient tree boosting, gradient boosted regression tree (GBRT)
      • GradientBoostingClassifier, GradientBoostingRegressor 사용
      • 축소 (shrinkage): learning_rate를 낮게 설정하고 많은 트리를 훈련하여 예측 성능을 상승시키는 규제
      • 확률적 그레디언트 부스팅 (stochastic gradient boosting): 각 트리가 훈련할 때 훈련 샘플의 비율을 지정하여 편향 상승 및 분산 감소
      • XGBoost (extreme gradient boosting): 최적화된 그레디언트 부스팅 라이브러리

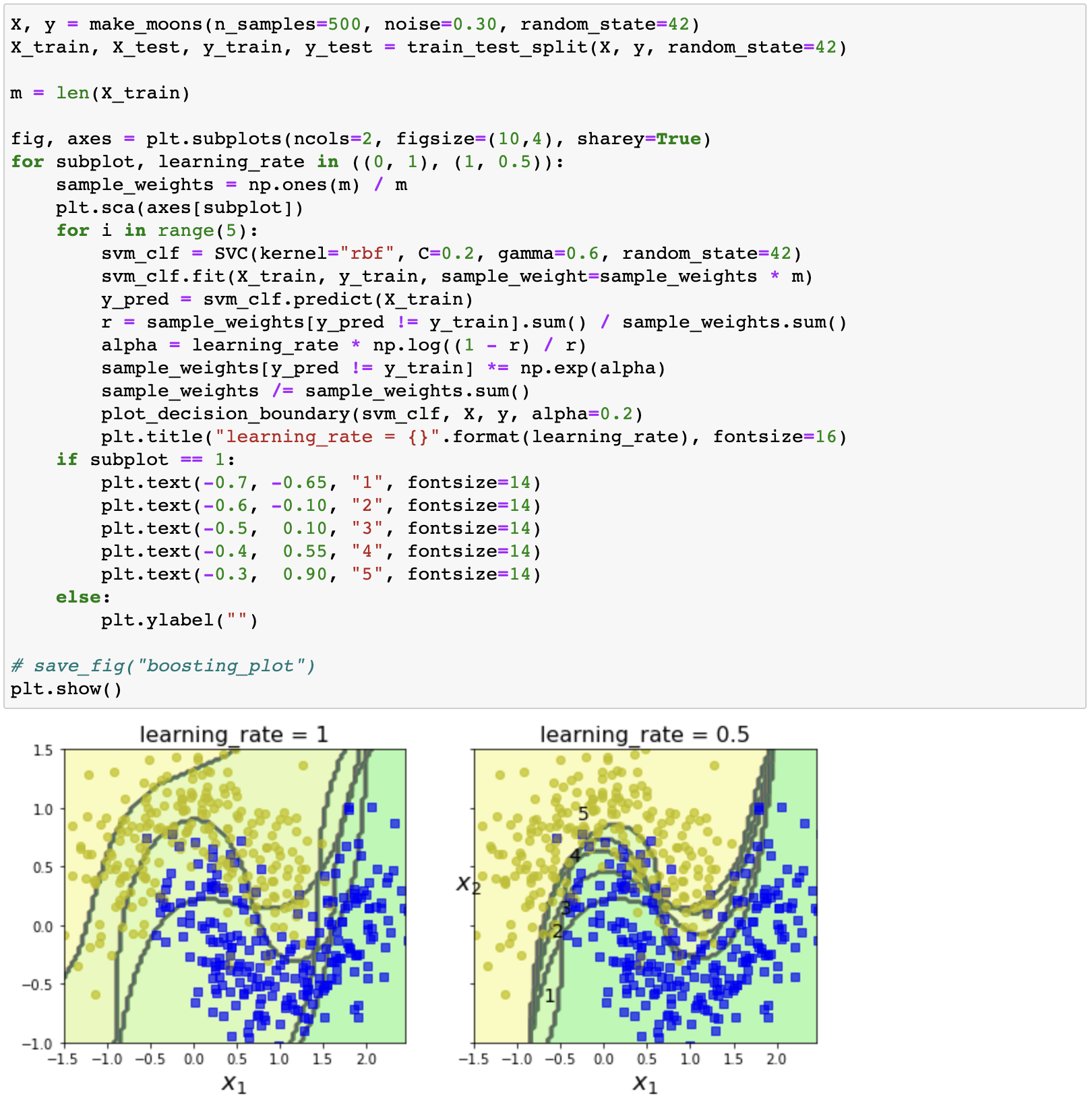
Decision boundaries of consecutive predictors
decision-boundaries-of-consecutive-predictors

Gradient boosting
gradient-boosting

Stacking

  • Stacking (stacked generalization): blender (meta learner)를 통해 각 모델의 예측을 취합하여 최종 예측 결정
  • Hold-out: blender를 학습시키는 일반적 방법
    1. 훈련 세트를 두 개의 서브셋으로 분리
    2. 첫 서브셋을 이용해 첫 번째 레이어의 에측 훈련
    3. 첫 번째 레이어의 예측기를 사용해 두 번째 (hold-out) 세트에 대한 예측 생성
    4. 생성된 예측을 blender의 훈련 세트로 사용

Dimensionality Reduction

Main Approaches for Dimensionality Reduction

  • Projection
    • 고차원 공간 안의 저차원 부분 공간 (subspace)에 투영하여 차원 축소
    • Swiss roll dataset과 같이 부분 공간이 뒤틀린 경우 뭉개질 수 있음
  • Manifold
    • $d$차원 매니폴드: 국부적으로 $d$차원 초평면으로 보일 수 있는 $n$차원 공간의 일부 ($d<n$)
      • Swiss roll dataset: $d=2,\ n=3$
    • 매니폴드 학습 (manifold learning): 훈련 샘플이 놓여있는 매니폴드를 모델링하는 과정
      • 실제 고차원 데이터셋이 더 낮은 저차원 매니폴드에 가깝게 놓여있다는 매니폴드 가정 (manifold assumption) 또는 매니폴드 가설 (manifold hypothesis)에 근거
  • 모델을 훈련시키기 전 훈련 세트의 차원을 감소시키면 훈련 속도는 빨라질 수 있지만 항상 모델의 성능이 향상되거나 간단해지는 것은 아님

PCA

  • PCA (Principal Component Analysis): 데이터에 가장 가까운 초평면 (hyperplane)을 정의하고 데이터를 투영
    • 주성분 (principal component, PC): 훈련 세트에서 분산이 최대인 축
    • $d$차원으로 투영: $\boldsymbol{X}_{d-proj}=\boldsymbol{X}\boldsymbol{W}_d$
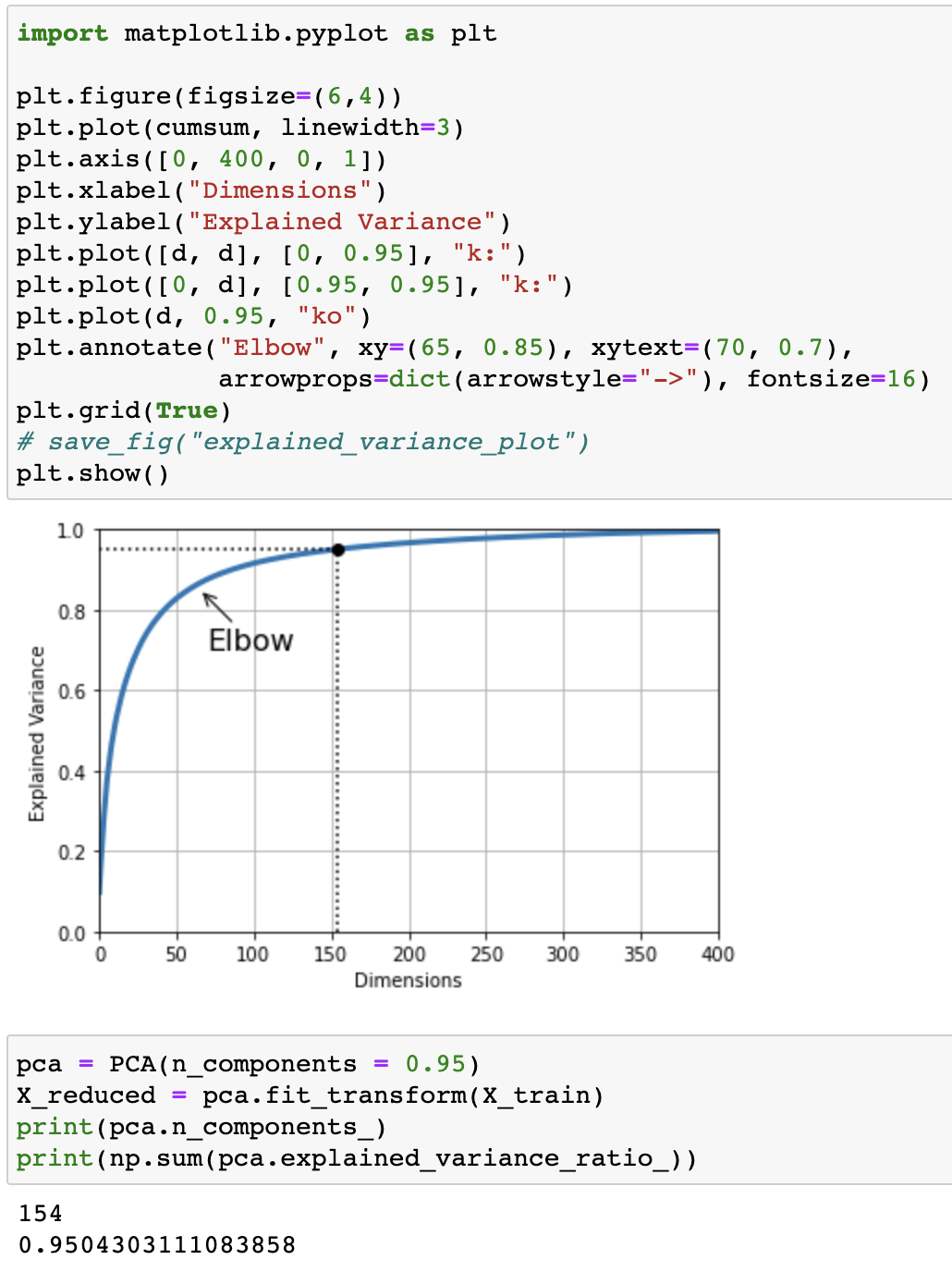
    • 설명된 분산의 비율 (explained variance ratio): pca.explained_variance_ratio_
  • 분산 보존: 저차원의 초평면에 훈련 세트를 투영하기 위한 초평면 선택 기준
    • 분산을 최대로 보존하여 정보 손실 최소화
1
2
3
4
from sklearn.decomposition import PCA

pca = PCA(n_components = 2)
X2D = pca.fit_transform(X)

Visualization of explained variance along dimensions and information on desired explaine variance
visualization-of-explained-variance-along-dimensions-and-information-on-desired-explaine-variance

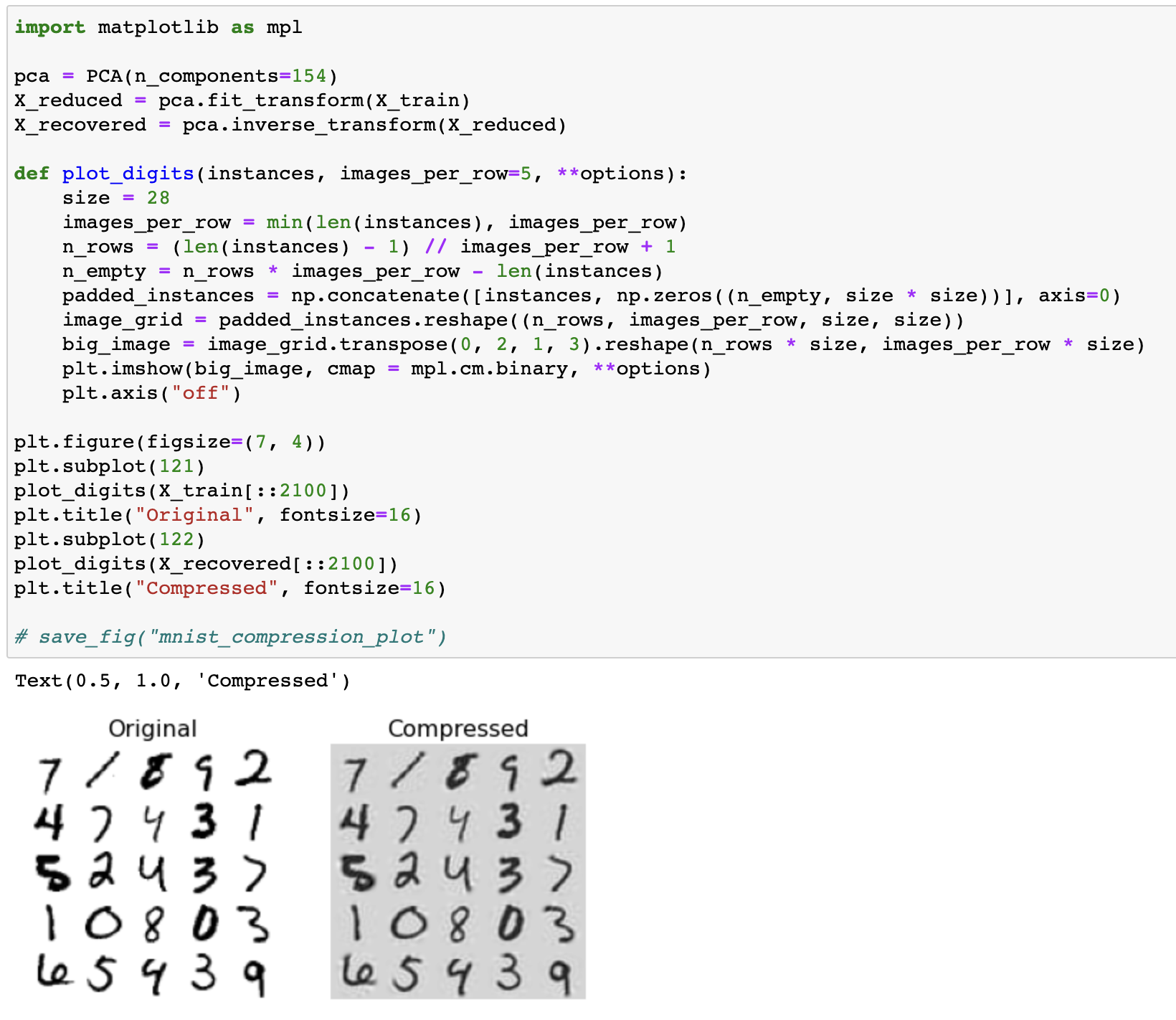
  • 재구성 오차 (reconstruction error): 원본 데이터와 재구성된 데이터 사이의 평균 제곱 거리
    • 원본의 차원 수로 되돌리는 PCA 역변환: $\boldsymbol{X}_{recovered}=\boldsymbol{X}_{d-proj}\boldsymbol{W}_d^T$

Original vs. Recover after compression
original-vs.-restore-after-compression

  • Random PCA: 확률적 알고리즘을 통해 처음 d개의 주성분에 대한 근삿값 도출
    • svd_solver 매개변수를 randomized로 지정
1
2
rnd_pca = PCA(n_components = 154, svd_solver = "randomized")
X_reduced = rnd_pca.fit_transform(X_train)
  • Incremental PCA (IPCA): 훈련 세트를 미니배치로 나눈 뒤 IPCA 알고리즘 적용
1
2
3
4
5
6
7
8
from sklearn.decomposition import IncrementalPCA

n_batches = 100
inc_pca = IncrementalPCA(n_components = 154)
for X_batch in np.array_split(X_train, n_batches):
    inc_pca.partial_fit(X_batch)
    
X_reduced = inc_pca.transform(X_train)
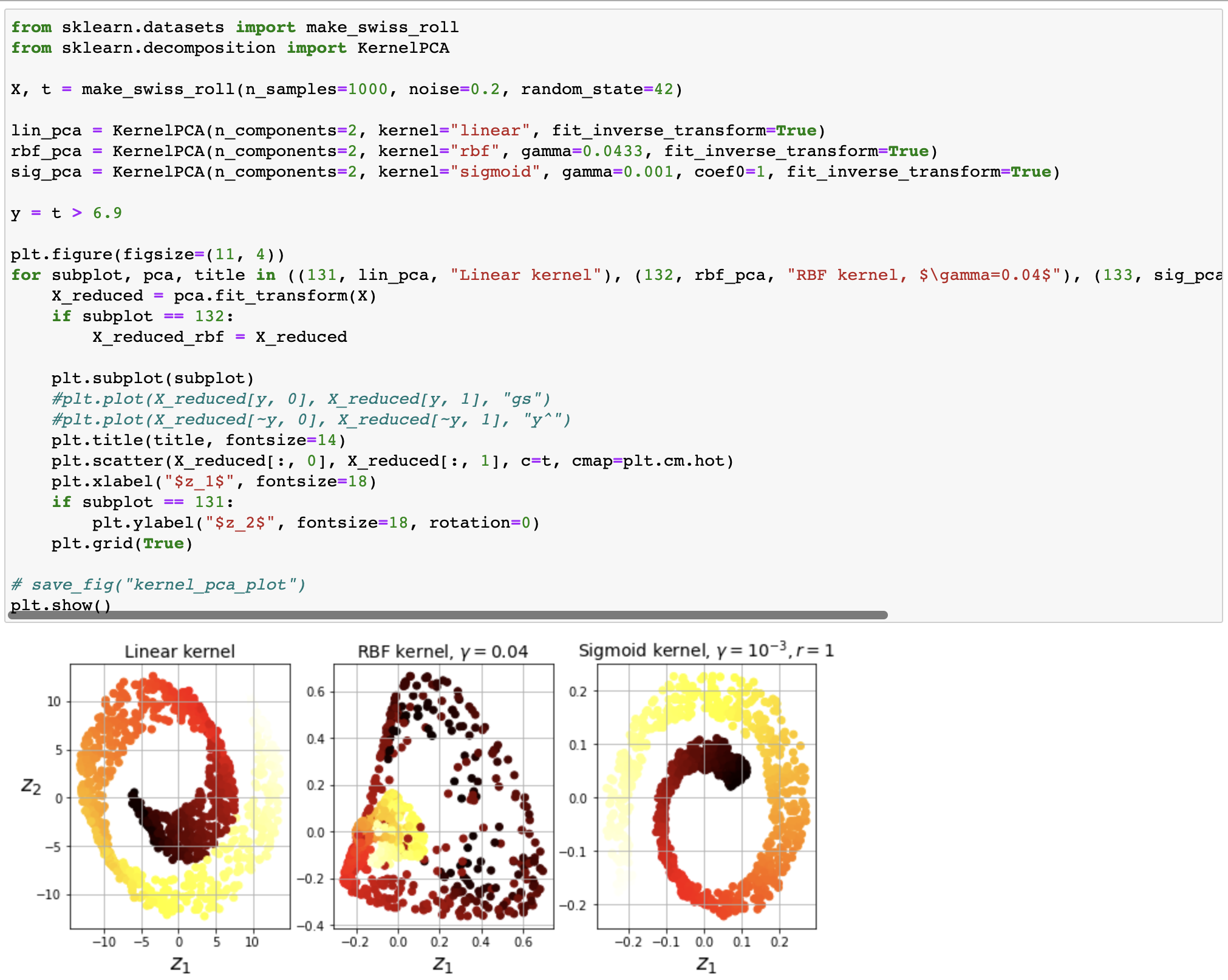
  • Kernel PCA (kPCA): kernel trick을 적용하여 차원 축소를 위한 복잡한 비선형 투영이 가능한 PCA
    • Kernel trick: 샘플을 매우 높은 고차원 공간인 특성 공간 (feature space)으로 매핑하는 수학적 기법
    • 투영된 뒤 샘플의 군집을 유지하거나 복잡한 매니폴드에 가까운 데이터셋을 펼칠 때 유리
1
2
3
4
from sklearn.decomposition import KernelPCA

rbf_pca = KernelPCA(n_components = 2, kernel = "rbf", gamma = 0.04)
X_reduced = rbf_pca.fit_transform(X)

Dimension reduction result according to kernel type
dimension-reduction-result-according-to-kernel-type

LLE

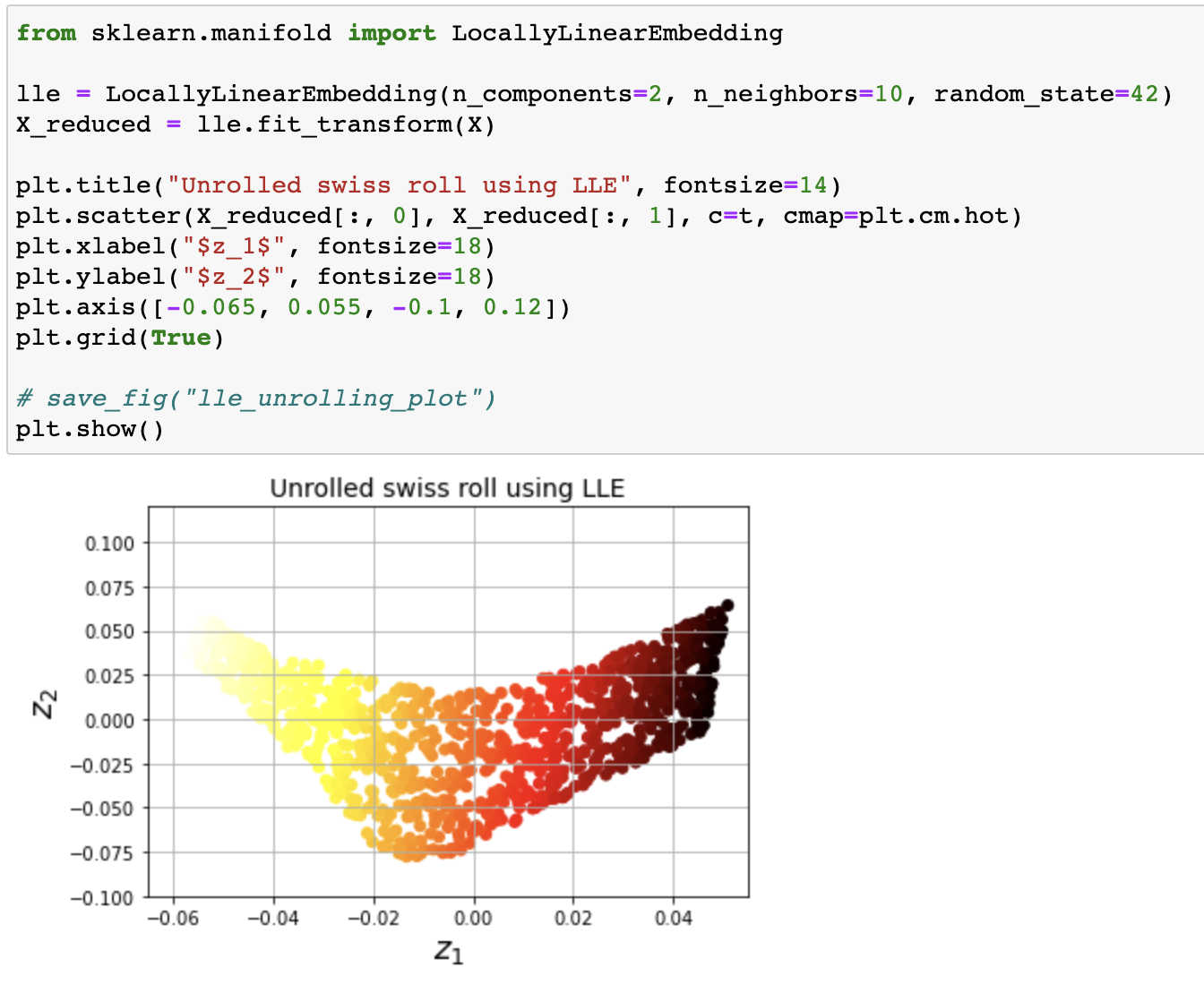
  • 지역 선형 임베딩 (locally linear embedding, LLE): 각 훈련 샘플이 가장 가까운 이웃 (closest neighbor, c.n.)에 대해 선형 연관성 파악 후 국부적 관계가 보존되는 저차원 표현 모색
    • 비선형 차원 축소 (nonlinear dimensionality reduction, NLDR)
    • 투영에 의존하지 않는 매니폴드 학습
    • 노이즈가 심하지 않은 꼬인 매니폴드에 유리

LLE applied to swiss roll dataset
lle-applied-to-swiss-roll-dataset

Etc.

  • 랜덤 투영 (random projection): 랜덤 선형 투영 기반 저차원 공간 투영
  • 다차원 스케일링 (multidimensional scailing, MDS): 샘플 간 거리 보존 및 차원 축소
  • Isomap: 가장 가까운 이웃과 연결 후 지오데식 거리 (geodesic distance)를 유지하머 차원 축소
  • t-SNE (t-distributed stochastic neighbor embedding): 비슷한 샘플은 가까이, 비슷하지 않은 샘플은 멀도록 차원 축소
  • 선형 판별 분석 (linear discriminant analysis, LDA): 훈련 과정에서 클래스 사이를 가장 잘 구분하는 축 규명 (supervised learning: classification)
1
2
3
4
5
6
7
8
9
10
11
12
from sklearn.manifold import MDS
from sklearn.manifold import Isomap
from sklearn.manifold import TSNE

mds = MDS(n_components=2, random_state=42)
X_reduced_mds = mds.fit_transform(X)

isomap = Isomap(n_components=2)
X_reduced_isomap = isomap.fit_transform(X)

tsne = TSNE(n_components=2, random_state=42)
X_reduced_tsne = tsne.fit_transform(X)

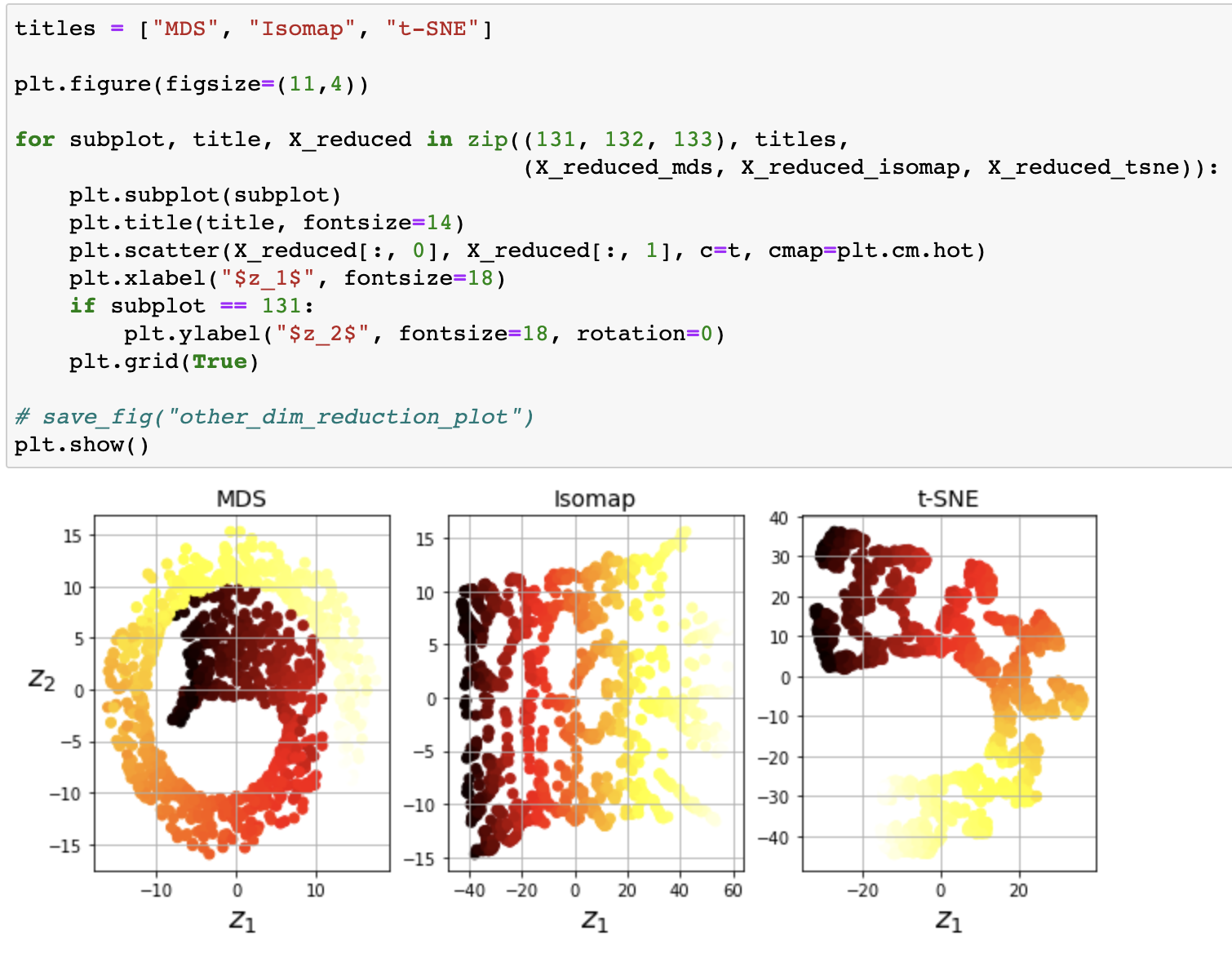
MDS vs. Isomap vs. t-SNE
mds-vs.-isomap-vs.-t-sne

Unsupervised Learning

  • 군집 (clustering): 비슷한 샘플을 클러스터 (cluster)로 수집
    • 고객 분류
    • 데이터 분석
    • 차원 축소 기법
    • 이상치 탐지
    • 준지도 학습
    • 검색 엔진
    • 이미지 분할
  • 이상치 탐지 (outlier detection): 정상 데이터의 경향 학습 후 비정상 샘플 감지
  • 밀도 추정 (density estimation): 데이터셋 생성 확률 과정 (random process)의 확률 밀도 함수 (probability density function, PDF) 추정

K-Means

  • K-means clustering algorithm: 주어진 데이터를 $k$개의 클러스터로 군집시키는 알고리즘
  • 군집에서 각 샘플의 레이블 (label): 알고리즘이 샘플에 할당한 클러스터의 인덱스
  • 보로노이 다이어그램 (Voronoi tessellation): 클러스터의 결정 경계 시각화
1
2
3
4
from sklearn.cluseter import KMeans

kmeans = KMeans(n_clusters = k)
y_pred = kmeans.fit_predict(X)
  • 하드 군집 (hard clustering): 샘플을 하나의 클러스터에 할당
  • 소프트 군집 (soft clustering): 클러스터마다 샘플에 점수 부여

DBSCAN

  • 알고리즘이 각 샘플에서 작은 거리인 $\varepsilon$ 내에 샘플의 수를 측정하고 해당 구역을 $\varepsilon$-이웃 ($\varepsilon$-neighbor)이라 명함
  • 핵심 샘플 (core instance): $\varepsilon$-이웃 내에 적어도 min_samples개의 샘플이 존재할 경우 해당 샘플을 의미
  • 핵심 샘플의 이웃에 존재하는 샘플을 모두 동일 클러스터로 분류
  • 이웃에는 다른 핵심 샘플이 포함될 수 있으며 핵심 샘플의 이웃의 이웃은 동일 클러스터 형성
  • 핵심 샘플 또는 이웃에 해당하지 않을 시 이상치로 분류
1
2
3
4
from sklearn.cluster import DBSCAN

dbscan = DBSCAN(eps = 0.05, min_samples = 5)
dbscan.fit(X)
  • labels_: 모든 샘플의 레이블
  • core_sample_indices_: 핵심 샘플의 인덱스
  • components_: 핵심 샘플 그 자체
  • predict() 대신 fit_predict() 제공: 새로운 샘플에 대해 클러스터 예측 불가
  • model.fit(dbscan.components_, dbscan.labels_[dbscan.core_sample_indices_])와 같은 방식으로 분류기 훈련 후 예측 가능