Hands-on Machine Learning (2)

Posted on In

Support Vector Machine (SVM)

  • Linear, nonlinear classification
  • Regression
  • Outlier detection

Linear SVM Classification

  • SVM Classifier: 각 클래스 사이에 가장 폭이 넓은 경계 정의 (large margin classification)
  • Support vector: 분류기의 경계에 위치한 훈련 데이터
    • 분류기의 경계 밖에 훈련 샘플을 더 추가해도 경계가 변화하지 않음

Soft Margin Classification

  • Hard margin classification: 모든 샘플이 경계 밖에 올바르게 분류되어 있는 경우
    • 데이터가 선형적으로 구분될 수 있어야 정상 작동
    • 이상치에 민감하여 일반화가 어려움
  • Soft margin classification: 마진 최대화와 마진 오류 (margin violation) 사이에 적절한 균형을 이루는 경우
    • Hyperparameter $C$
      • Low $C$: 마진 오류 증가, 일반화 성능 향상
      • High $C$: 마진 오류 감소, 일반화 성능 감소
      • SVM 모델이 과대적합인 경우 $C$를 감소시켜 모델을 규제할 수 있음
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import numpy as np
from sklearn import datasets
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.svm import LinearSVC
# from sklearn.linear_model import SGDClassifier

iris = datasets.load_iris()
X = iris["data"][:, (2, 3)]
y = (iris["target"] == 2).astype(np.float64)

svm_clf = Pipeline([
    ("scaler", StandardScaler()),
    ("linear_svc", LinearSVC(C = 1, loss = "hinge"))
#     ("linear_svc", SGDClassifier(loss = "hinge", alpha = 1 / (len(X) * 1)))
])

svm_clf.fit(X, y)

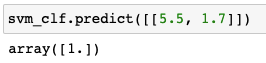
Classification of trained SVM model
Classification of trained SVM model

Nonlinear SVM Classification

1
2
3
4
5
6
7
8
9
10
11
12
from sklearn.datasets import make_moons
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures

X, y = make_moons(n_samples = 1000, noise = 0.15)
polynomial_svm_clf = Pipeline([
    ("poly_features", PolynomialFeatures(degree = 3)),
    ("scaler", StandardScaler()),
    ("svm_clf", LinearSVC(C = 10, loss = "hinge"))
])

polynomial_svm_clf.fit(X, y)

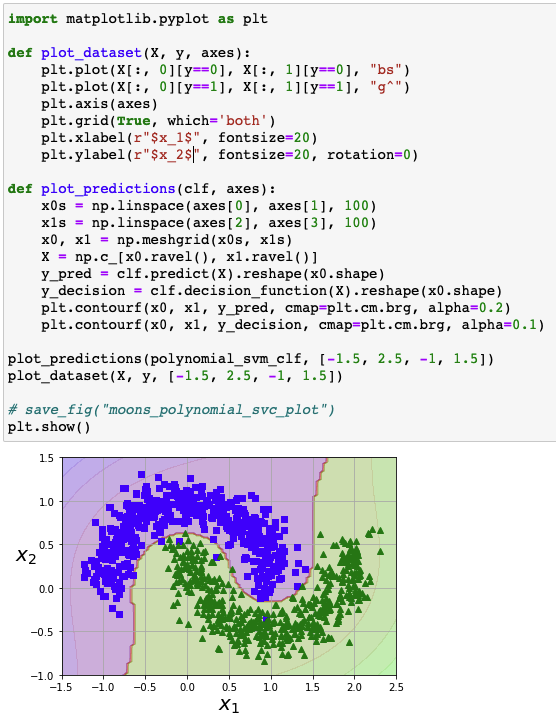
Linear SVM classifier based on polynomial features
Linear SVM classifier based on polynomial features

Polynomial Kernel

  • Polynomial features: 간단하고 다양한 머신러닝 알고리즘에서 적합
    • 복잡한 데이터셋에 대해 한계점 존재
    • 높은 차수의 다항식이 생성될 경우 모델의 속도 저하 발생
  • Kernel trick: 실제로 특성을 추가하지 않고 수학적 전개를 통해 비선형 분류
1
2
3
4
5
6
7
from sklearn.svm import SVC

poly_kernel_svm_clf = Pipeline([
    ("scaler", StandardScaler()),
    ("svm_clf", SVC(kernel = "poly", degree = 3, coef0 = 1, C = 5))
])
poly_kernel_svm_clf.fit(X, y)
  • 3차 다항식 커널 이용
  • 모델의 과대적합 발생 $\rightarrow$ 커널의 차수 감소
  • 모델의 과소적합 발생 $\rightarrow$ 커널의 차수 증가
  • coef0: 모델이 높은 차수와 낮은 차수에 얼마나 영향을 받을지 조절하는 hyperparameter

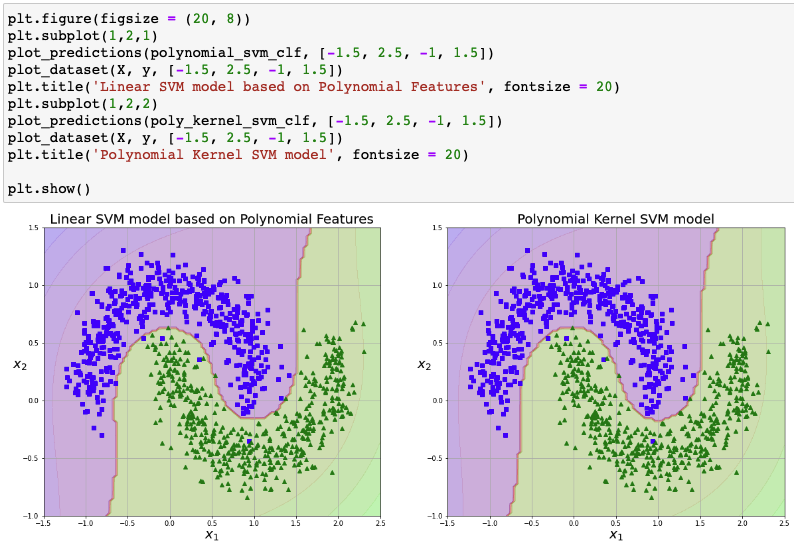
Linear SVM model based on Polynomial Features vs. Polynomial Kernel SVM model
스크린샷 2022-07-25 오후 9 08 44

Adding Similarity Features

  • 유사도 함수 (similarity function): 각 샘플이 특정 랜드마크와 얼마나 닮았는지 측정

Gaussian RBF (Radial Basis Function)
$$
\phi_\gamma(\boldsymbol{x},l)=\exp{(-\gamma||\boldsymbol{x}-l||^2)}
$$

1
2
def gaussian_rbf(x, landmark, gamma):
    return np.exp(-gamma * np.linalg.norm(x - landmark, axis=1)**2)

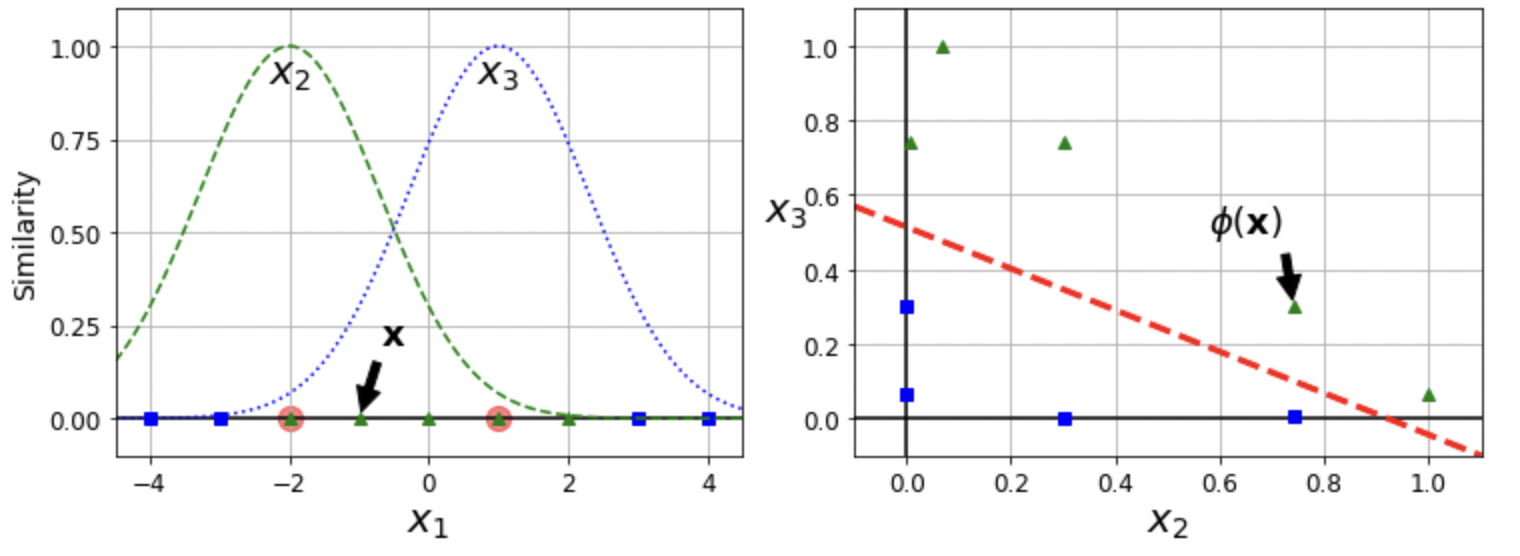
Improved linear classification through Gaussian RBF
Improved linear classification through Gaussian RBF

  • Landmark: $x_1=-2$ (green), $x_1=1$ (blue)
  • Sample $x_1=-1$ $\rightarrow$ $x_2=\exp(-0.3\times1^2)\approx0.74$, $x_3=\exp(-0.3\times2^2)\approx0.30$
    • $\gamma = 0.3$
    • 훈련 세트의 차원을 수학적으로 확대하여 선형 분류성 향상

Gaussian RBF Kernel

1
2
3
4
rbf_kernel_svm_clf = Pipeline([
        ("scaler", StandardScaler()),
        ("svm_clf", SVC(kernel = "rbf", gamma = 0.1, C = 10))
    ])

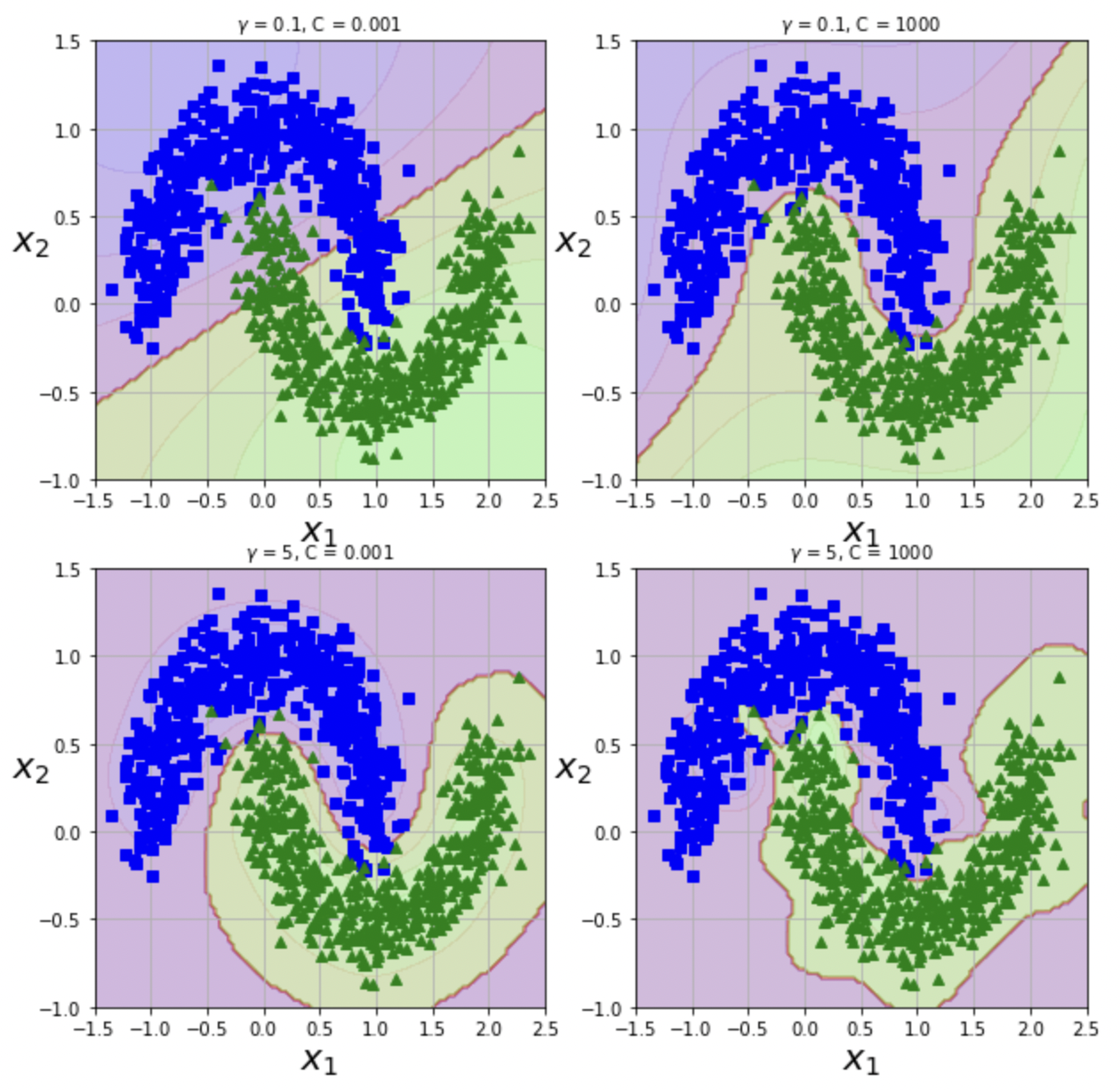
Gaussian SVM according to hyperparameters
Gaussian SVM according to hyperparameters

  • Hyperparameter $\gamma$
    • Low $\gamma$: 결정 경계가 상대적으로 규칙적이고 부드러움
    • High $\gamma$: 결정 경계가 상대적으로 불규칙하고 구부러짐
Class Time complexity Out-of-core support Scaling required Kernel trick
LinearSVC $O(m\times n)$ X O X
SGDClassifier $O(m\times n)$ O O X
SVC $O(m^2\times n)$ to $O(m^3\times n)$ X O O

SVM Regression

1
2
3
4
5
6
7
8
9
10
11
from sklearn.svm import LinearSVR

svm_reg = LinearSVR(epsilon = e)
svm_reg.fit(X, y)

...

from sklearn.svm import SVR

svm_poly_reg = SVR(kernel = "poly", degree = N, C = c, epsilon = e)
svm_poly_reg.fit(X, y)

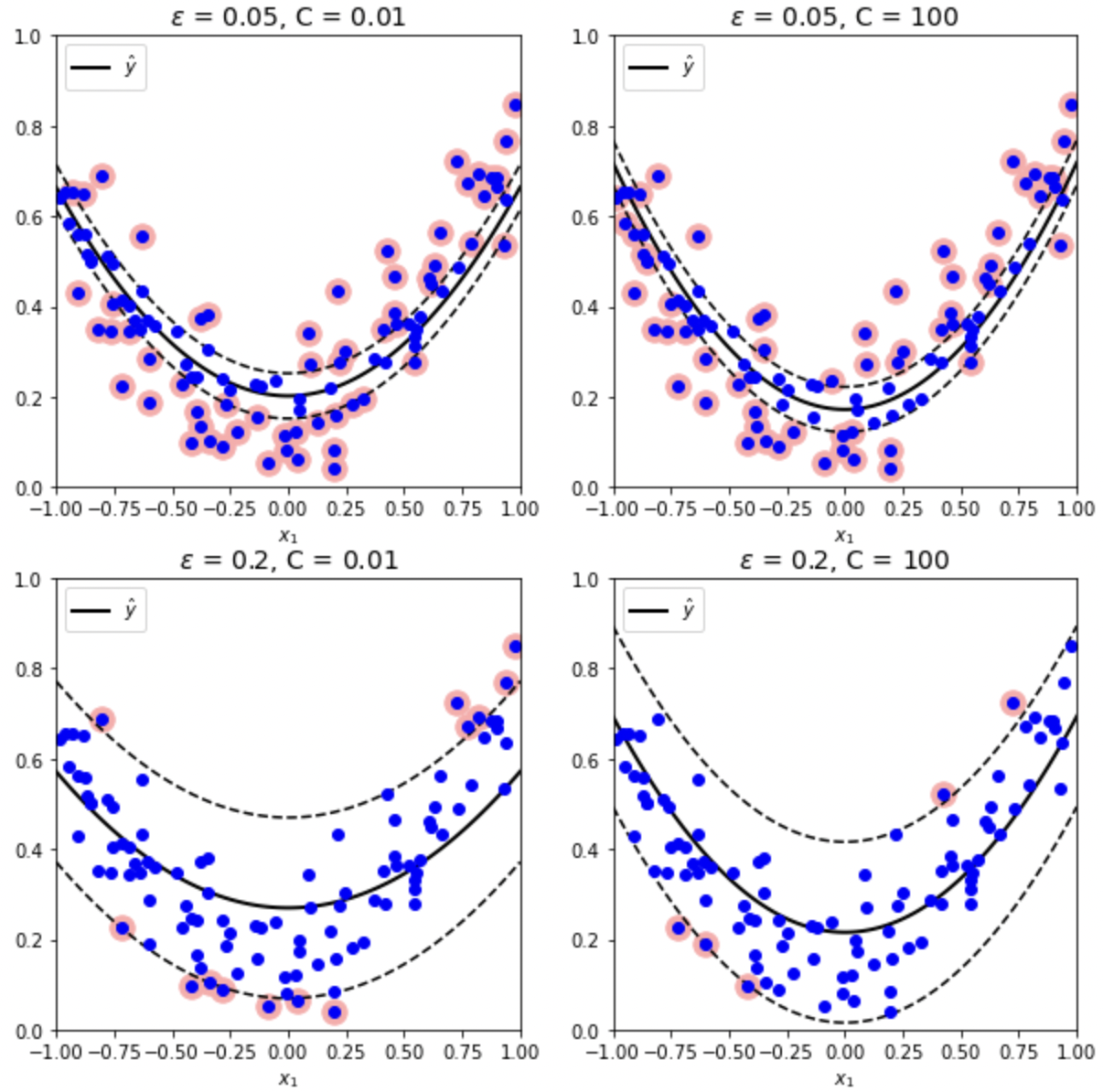
SVM Regression according to hyperparameters
SVM Regression according to hyperparameters

  • SVM Regression: 제한된 마진 오류 내에서 마진이 포함하는 샘플 최대화
    • Hyperparameter $\varepsilon$: 마진의 폭 설정
    • Hyperparameter $C$:
      • Low $C$: 마진 오류에 대한 규제 강화 (마진 오류 증가)
      • High $C$: 마진 오류에 대한 규제 약화 (마진 오류 감소)

SVM Theory

  • Notation
    • $\theta_0,\ b$: 편향 (bias)
    • $\theta_1$ ~ $\theta_n,\ \boldsymbol{w}$: 가중치 (weight)
  • Linear SVM Classifier
    • 결정 함수: $\boldsymbol{w}^T\boldsymbol{x}+b=w_1x_1+…+w_nx_n+b$ $\rightarrow$ class prediction
      • 결정 함수 $>$ 0: $\hat{y}$ = positive class (1)
      • 결정 함수 $\leq$ 0: $\hat{y}$ = negative class (0)
    • Training: 설정된 마진의 조건 (하드 마진 / 소프트 마진)을 만족하면서 마진을 최대화 시키는 $\boldsymbol{w},\ b$를 산출해내는 과정
    • 목적 함수
      • 결정 함수의 기울기 = 가중치 벡터의 노름 ($||\boldsymbol{w}||$)
      • $||\boldsymbol{w}||$이 작을수록 마진 증가
      • $\therefore$ 마진을 최대화하기 위해 $||\boldsymbol{w}||$ 최소화
    • 하드 마진 선형 SVM 분류기의 목적 함수: $\underset{\boldsymbol{w},b}{\operatorname{minimize}}\frac{1}{2}\boldsymbol{w}^T\boldsymbol{w}$ (if $i=1,2,…,m\ \rightarrow\ t^{(i)}(\boldsymbol{w}^T\boldsymbol{x}^{(i)}+b)\geq 1$)
    • 소프트 마진 선형 SVM 분류기의 목적 함수: $\underset{\boldsymbol{w},b,\zeta}{\operatorname{minimize}}\frac{1}{2}\boldsymbol{w}^T\boldsymbol{w}+C\Sigma_{i=1}^m\zeta^{(i)}$ (if $i=1,2,…,m\ \rightarrow\ t^{(i)}(\boldsymbol{w}^T\boldsymbol{x}^{(i)}+b)\geq 1-\zeta^{(i)},\ \zeta^{(i)}\geq0$)
  • Kernel SVM
    • Linear: $K(\boldsymbol{a,b})=\boldsymbol{a}^T\boldsymbol{b}$
    • Polynomial: $K(\boldsymbol{a,b})=(\gamma\boldsymbol{a}^T\boldsymbol{b}+r)^d$
    • Gaussian RBF: $K(\boldsymbol{a,b})=\exp{(-\gamma||\boldsymbol{a}-\boldsymbol{b}||^2)}$
    • Sigmoid: $K(\boldsymbol{a,b})=\tanh{\gamma\boldsymbol{a}^T\boldsymbol{b}+r}$

Decision Tree

  • Classification
  • Regression
  • Multioutput tasks

Training and Visualization

1
2
3
4
from sklearn.tree import DecisionTreeClassifier

tree_clf = DecisionTreeClassifier(max_depth = N, random_state = 42)
tree_clf.fit(X, y)

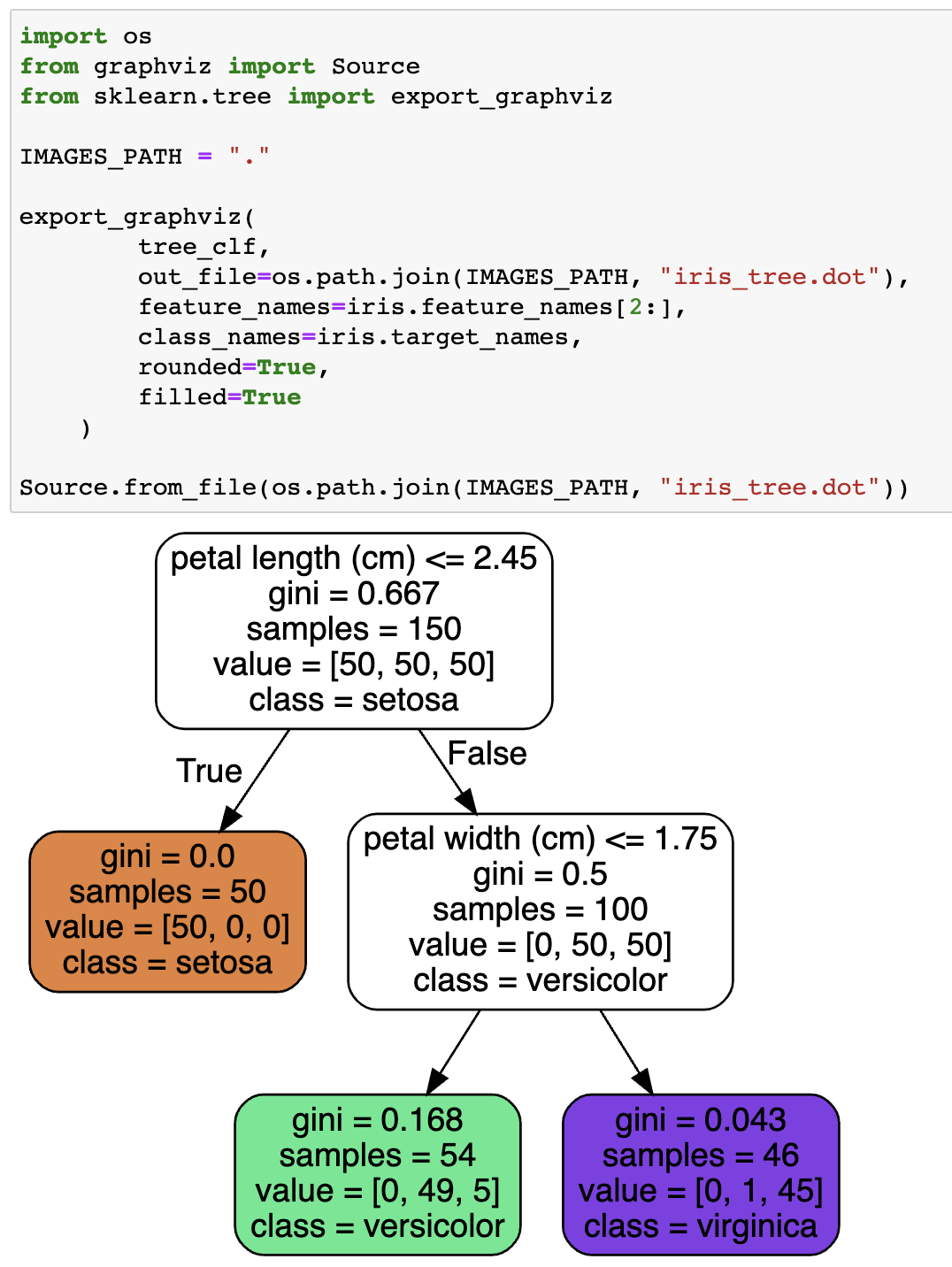
Visualization
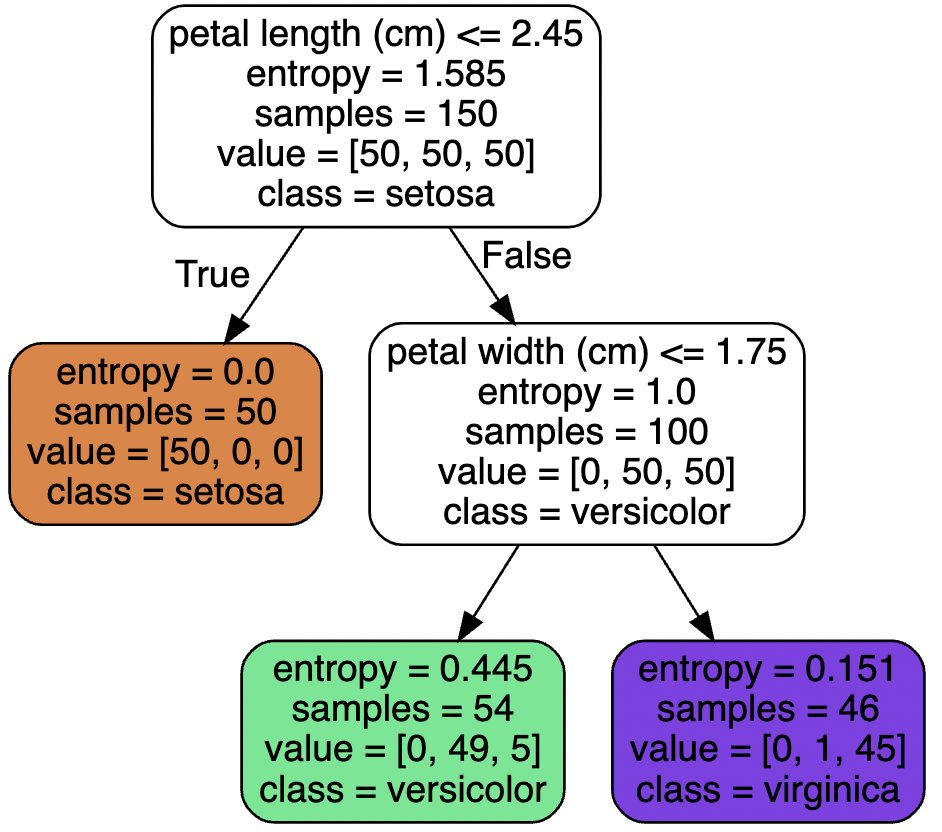
Visualization

Prediction

  • Root node: 깊이가 0인 최상위 노드
  • Leaf node: Child node를 가지지 않는 노드
  • Gini: 불순도 (impurity) 측정 값
    • 모든 샘플이 같은 클래스 $\rightarrow$ gini = 0

Gini impurity
$$
G_i=1-\Sigma^n_{k=1}p_{i,k}^2
$$

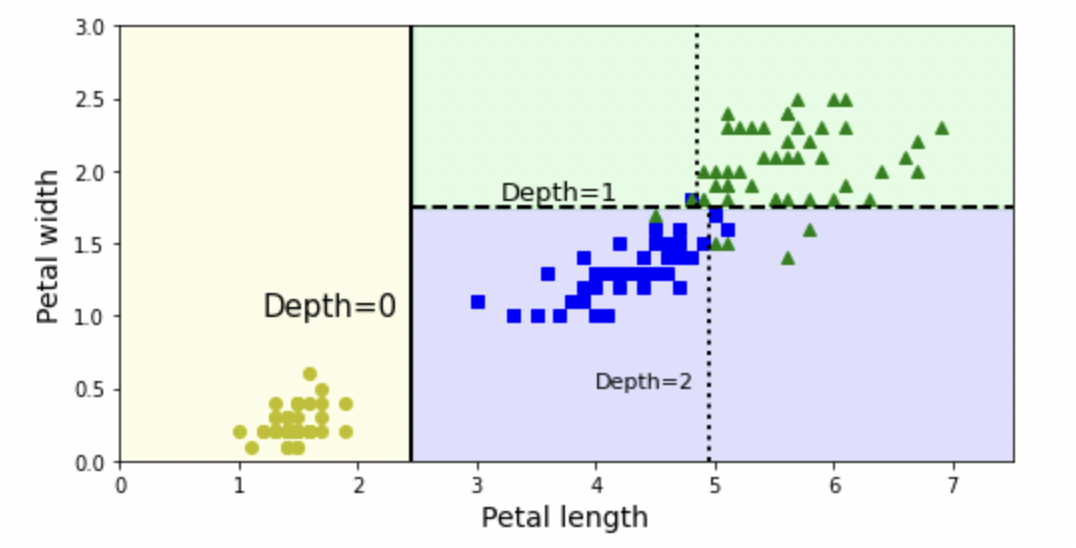
Decision boundaries
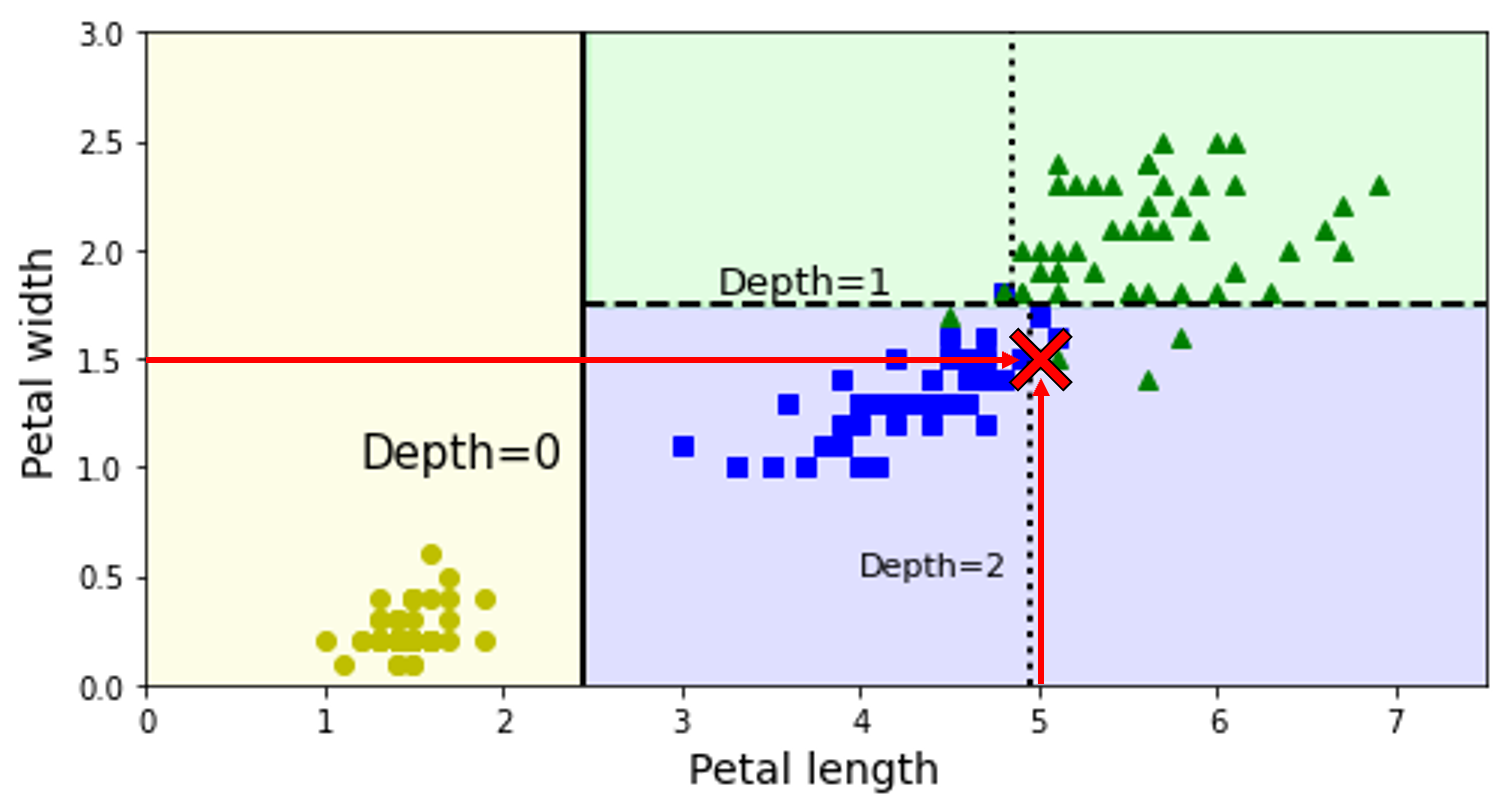
Decision boundaries

Estimating Class Probabilities

Class estimation process
Class estimation process_1
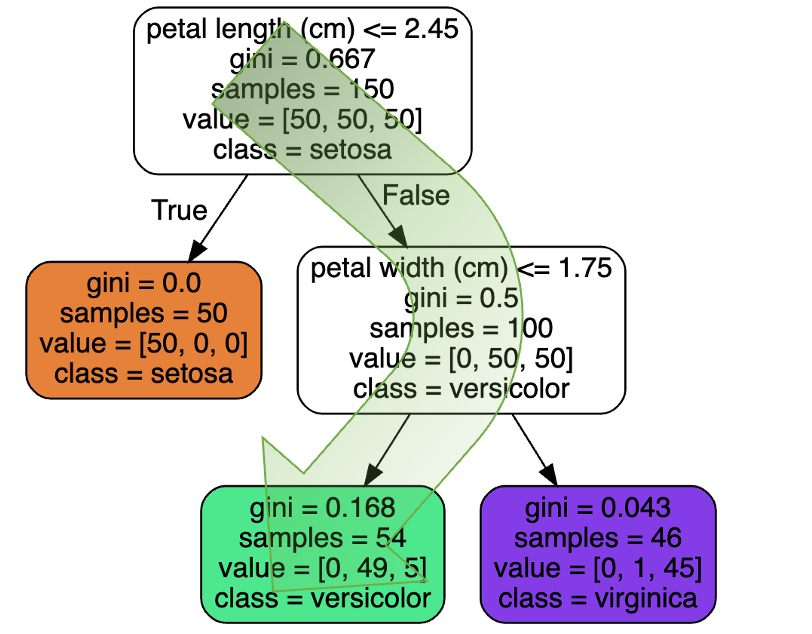
Class estimation process_2
Class estimation process_3

  • $0\%=0/54\times100$
  • $90.7\%=49/54\times100$
  • $9.3\%=5/54\times100$

CART Training Algorithm

  • CART (Classification And Regression Tree)
    1. 하나의 특성 $k$의 임계값 $t_k$를 사용하여 두개의 서브셋으로 나눔
    2. 하단의 비용 함수 최소화 (가장 순수한 서브셋으로 나눌 수 있는 $(k,t_k)$ 짝 도출)
    3. 나누어진 서브셋에 대해 최대 깊이 만큼 위의 절차 반복 (불순도 감소 불가 시 정지)

CART cost function for classification
$$
J(k,t_k)=\frac{m_{left}}{m}G_{left}+\frac{m_{right}}{m}G_{right}
$$

  • $G_{left/right}$: 좌측/우측 서브셋의 불순도
  • $m_{left/right}$: 좌측/우측 서브셋의 샘플 수

Computational Complexity

결정 트리를 탐색하기 위한 계산 복잡도
$$
O(\log_2(m))
$$

각 노드에서 모든 훈련 샘플의 모든 특성 비교 시 계산 복잡도
$$
O(n\times m\log_2(m))
$$

Entropy Impurity

  • criterion = "entropy": 지니 불순도 대신 엔트로피 불순도 사용
    • 한 서브셋 내의 모든 샘플의 클래스가 동일 $\rightarrow\ H_i=0$
  • Vs. Gini Impurity
    • 큰 차이는 존재하지 않음
    • 지니 불순도의 계산 속도
    • 다른 트리가 만들어 질 때 엔트로피가 더 균형잡힘

$$
H_i=-\overset{n}{\underset{p_{i,k}\neq0}{\underset{k=1}{\Sigma}}} p_{i,k}\log_2(p_{i,k})
$$

Entropy Impurity
Entropy Impurity

Regularization Hyperparameters

  • Nonparametric model (비파라미터 모델): 훈련되기 전 파라미터의 수가 결정되지 않는 모델 (과대적합 위험 존재)
  • Parametric model (파라미터 모델): 모델 파라미터의 수가 미리 정의 (과소적합 위험 존재)
  • Regularization hyperparameter (규제 매개변수): 훈련 데이터에 대한 과대적합을 피하기 위해 학습할 때 모델의 자유도 제한
  • DecisionTreeClassifier
    • max_depth: 결정 트리의 깊이 (기본값 = None, 제한 없음)
    • min_samples_split: 분할되기 위해 노드가 가져야하는 최소 샘플 수
    • min_samples_leaf: 리프 노드가 가지고 있어야할 최소 샘플 수
    • min_weight_fraction_leaf: 가중치가 부여된 전체 샘플 수에서의 비율
    • max_leaf_nodes: 리프 노드의 최대 수
    • max_features: 각 노드에서 분할에 사용할 특성의 최대 수

Regression

1
2
3
4
from sklearn.tree import DecisionTreeRegressor

tree_reg = DecisionTreeRegressor(max_depth = N)
tree_reg.fit(X, y)

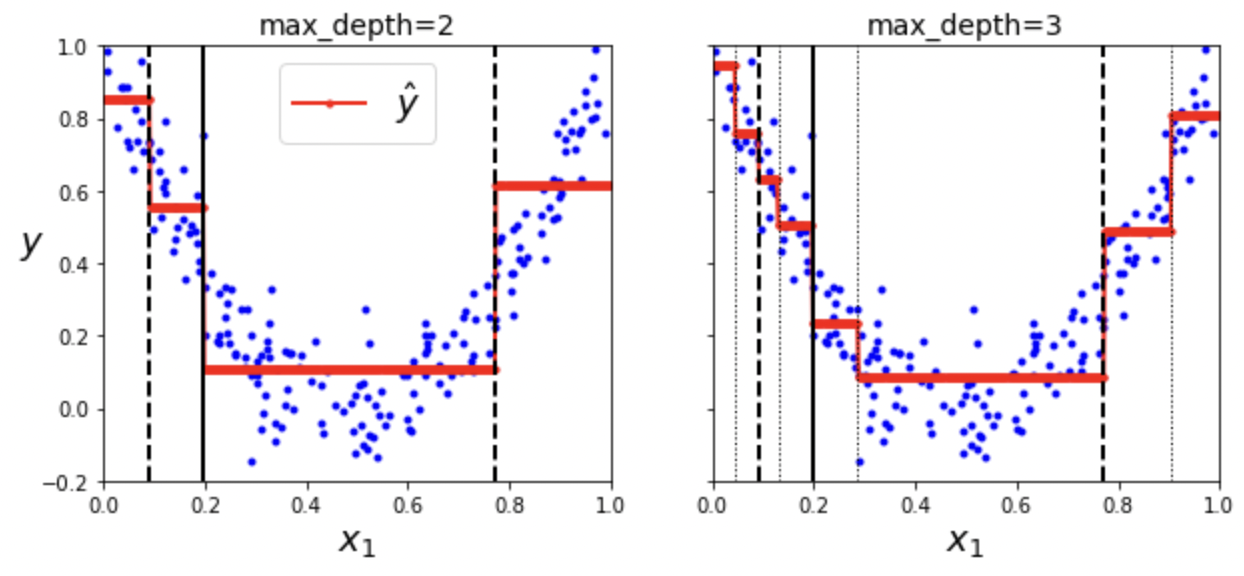
Decision Tree Regression
Decision Tree Regression

  • 각 노드에서 값 예측
  • 각 영역의 예측값은 그 영역에 있는 훈련 데이터의 평균

CART cost function for regression
$$
J(k,t_k)=\frac{m_{left}}{m}MSE_{left}+\frac{m_{right}}{m}MSE_{right}
$$

  • $MSE_{node}=\underset{i\in node}{\Sigma}(\hat{y}_{node}-y^{(i)})^2$
  • $\hat{y}_{node}=\frac{1}{m_{node}}\underset{i\in node}{\Sigma}y^{(i)}$

Limitation

훈련 데이터의 회전과 작은 변화에 민감 $\rightarrow$ Random Forest 모델을 통해 개선