Hands-on Machine Learning (1)

Posted on In

Setting up development environment

Clone source code

Ref: Hands-on Machine Learning

1
git clone https://github.com/rickiepark/handson-ml2.git

Download Anaconda

1
2
conda --version
conda update conda
Anaconda

Download Jupyter Notebook

Set environment

1
2
3
conda env create -f environment.yml
conda activate tf2
python -m ipykernel install --user --name=python3
Environment 
1
jupyter notebook

Setting complete

Setting complete

Machine Learning

Definition of Machine Learning: The science (and art) of programming computers so they can learn from data

  • Supervised Learning: The training data you feed to the algorithm includes the desired solutions, called labels
    • Classification
      • k-Nearest Neighbors (kNN)
      • Linear Regression
      • Logistic Regression
      • Support Vector Machines (SVM)
      • Decision Trees and Random Forests
      • Neural Networks
    • Regression
      • k-Nearest Neighbors (kNN)
      • Linear Regression
      • Logistic Regression
      • Support Vector Machines (SVM)
      • Decision Trees and Random Forests
      • Neural Networks
  • Unsupervised Learning: The training data is unabled
    • Clustering
      • K-Means
      • DBSCAN
      • Hierarchical Cluster Analysis (HCA)
    • Anomaly detection and novelty detection
      • One-class SVM
      • Isolation Forest
    • Visualization and dimensionality reduction
      • Principal Component Analysis (PCA)
      • Kernel PCA
      • Locally-Linear Embedding (LLE)
      • t-distributed Stochastic Neighbor Embedding (t-SNE)
    • Association rule learning
      • Apriori
      • Eclat
  • Semi-supervised Learning: Dealing with partially labeled training data, usually a lot of unlabeled data and a little bit of labeled data
    • Deep Belief Networks (DBNs)
    • Restricted Boltzmann Machines (RBMs)
  • Reinforcement Learning: How intelligent agents ought to take actions in an environment in order to maximize the notion of cumulative reward

Classification

Training a Binary Classifier

1
2
3
4
5
6
from sklearn.linear_model import SGDClassifier

sgd_clf = SGDClassifier(random_state = N)
sgd_clf.fit(X_train, y_train)

sgd_clf.predict(y_test)

Performance Measures

Confusion Matrix

Predicted: Negative Pridicted: Positive
Actual: Negative True Negative (TN) False Positive (FP)
Actual: Positive False Negative (FN) True Positive (TP) 
1
2
3
4
5
from sklearn.model_selection import cross_val_predict
from sklearn.metrics import confusion_matrix

y_train_pred = cross_val_predict(sgd_clf, X_train, y_train, cv = N)
confusion_matrix(y_train, y_train_pred)

$$
precision = \frac{TP}{TP + FP}
$$

1
2
3
from sklearn.metrics import precision_score

precision_score(y_train, y_train_pred)

$$
recall = \frac{TP}{TP + FN}
$$

1
2
3
from sklearn.metrics import recall_score

recall_score(y_train, y_train_pred)

$$
F_1 = 2\times\frac{precision\times recall}{precision+recall}
$$

1
2
3
from sklearn.metrics import f1_score

f1_score(y_train, y_train_pred)

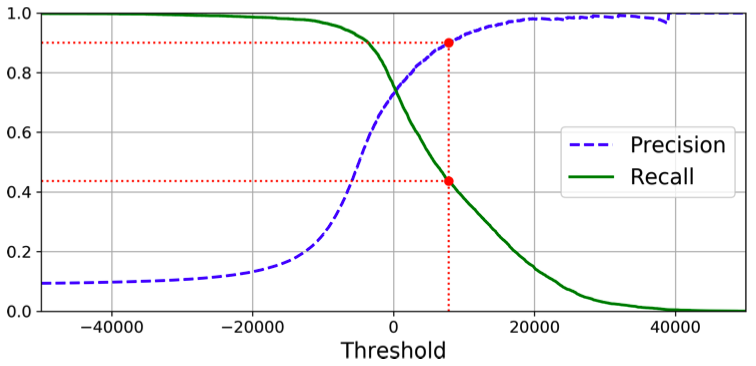
Precision and recall versus the decision threshold (precision/recall tradeoff)
Precision and recall versus the decision threshold (precision/recall tradeoff)

1
2
3
4
from sklearn.metrics import precision_recall_curve

y_scores = sgd_clfd.decision_function(testData)
precisions, recalls, thresholds = precision_recall_curve(y_train, y_scores)

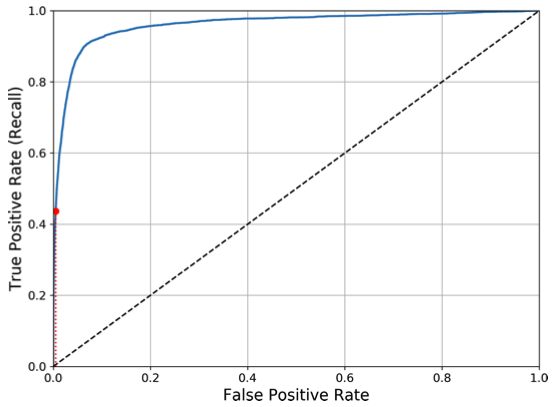
ROC (Receiver Operating Characteristic) curve
ROC curve

1
2
3
from sklearn.metrics import roc_curve

fpr, tpr, thresholds = roc_curve(y_train, y_scores)

ROC AUC (Area Under the Curve)

1
2
3
from sklearn.metrics import roc_auc_score

roc_auc_score(y_train, y_scores)

Multiclass Classification

One-versus-All (OvA)

  • $N$ Classifiers
1
sgd_clf.fit(X_train, y_train)

One-versus-One (OvO)

  • $N\times(N-1)/2$ Classifiers
1
2
3
4
5
from sklearn.multiclass import OneVsOneClassifier

ovo_clf = OneVsOneClassifier(SGDClassifier(random_state = 42))
ovo_clf.fit(X_train, y_train)
ovo_clf.predict(testData)

Scaling the inputs

1
2
3
4
5
6
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import cross_val_score

scaler = StandardScaler
X_train_scaled = scaler.fit_transform(X_train.astype(np.fload64))
cross_val_score(sgd_clf, X_train_scaled, y_train, cv = N, scoring = "accuracy")

Error Analysis

1
2
3
4
5
y_train_pred = cross_val_predict(sgd_clf, X_trained_scaled, y_train, cv = N)
conf_mx = confusion_matrix(y_train, y_train_pred)

plt.matshow(conf_mx, cmap = plt.cm.gray)
plt.show()

Multioutput Classification

1
2
knn_clf.fit(X_train, y_train)
y_pred = knn_clf.predict(testData)

Training Models

Linear Regression

Linear regression model prediction

$$
\hat{y}=\theta_0+\theta_1x_1+\theta_2x_2+…+\theta_nx_n
$$

$$ \hat{y}=h_{\boldsymbol{\theta}}(\boldsymbol{x})=\boldsymbol{\theta}\cdot\boldsymbol{x} $$
  • $\hat{y}$: Predicted value
  • $n$: The number of features
  • $x_i$: The $i^{th}$ feature value
  • $\theta_j$: The $j^{th}$ model parameter

Mean Square Error (MSE) cost function for a linear regression model

$$
MSE(\boldsymbol{X}, h_{\boldsymbol{\theta}})=\frac{1}{m}\Sigma^m_{i=1}(\boldsymbol{\theta}^T\boldsymbol{x}^{(i)}-y^{(i)})^2
$$

Gradient Descent

Partial derivatives of the cost function

$$
\frac{\partial}{\partial\theta_j}MSE(\boldsymbol{\theta})=\frac{2}{m}\Sigma^m_{i=1}(\boldsymbol{\theta}^T\boldsymbol{x}^{(i)}-y^{(i)})x^{(i)}_j
$$

Gradient vector of the cost function

$$
\nabla_{\boldsymbol{\theta}}MSE(\boldsymbol{\theta})=\frac{2}{m}\boldsymbol{X}^T(\boldsymbol{X\theta-y})
$$

Gradient descent step

$$
\boldsymbol{\theta}^{(next\ step)}=\boldsymbol{\theta}-\eta\nabla_{\boldsymbol{\theta}}MSE(\boldsymbol{\theta})
$$

Polynomial Regression

1
2
3
4
from sklearn.preprocessing import PolynomialFeatures

poly_features = PolynomialFeatures(degree = N, include_bias = False)
X_poly = poly_features.fit_transform(X)

Ridge Regression

Ridge regression cost function

$$
J(\boldsymbol{\theta})=MSE(\boldsymbol{\theta})+\alpha\frac{1}{2}\Sigma^n_{i=1}\theta_i^2
$$

1
2
3
4
5
from sklearn.linear_model import Ridge

ridge_reg = Ridge(alpha = 1, solver = "cholesky")
ridge_reg.fit(X, y)
ridge_reg.predict([[N]])

Lasso Regression

Lasso regression cost function

$$
J(\boldsymbol{\theta})=MSE(\boldsymbol{\theta})+\alpha\Sigma^n_{i=1}|\theta_i|
$$

1
2
3
4
5
from sklear.linear_model import Lasso

lasso_reg = Lasso(alpha = 0.1)
lasso_reg.fit(X, y)
lasso_reg.predict([[N]])

Elastic Net

Elastic net cost function

$$
J(\boldsymbol{\theta})=MSE(\boldsymbol{\theta})+r\alpha\Sigma^n_{i=1}|\theta_i|+\frac{1-r}{2}\alpha\frac{1}{2}\Sigma^n_{i=1}\theta_i^2
$$

1
2
3
4
5
from sklearn.linear_model import ElasticNet

elastic_net = ElasticNet(alpha = 0.1, l1_ratio = 0.5)
elastic_net.fit(X, y)
elastic_net.predict([[N]])

Logistic Regression

Logistic regression model estimated probability

$$
\hat{p}=h_{\boldsymbol{\theta}}(\boldsymbol{x})=\sigma(\boldsymbol{x}^T\boldsymbol{\theta})
$$

Logistic function

$$
\sigma(t)=\frac{1}{1+e^{-t}}
$$

Logistic regression cost function (log loss)

$$
J(\boldsymbol{\theta})=-\frac{1}{m}\Sigma^m_{i=1}[y^{(i)}log(\hat{p}^{(i)})+(1-y^{(i)})log(1-\hat{p}^{(i)})]
$$

1
2
3
4
5
6
from sklearn.linear_model import LogisticRegression

log_reg = LogisticRegression()
log_reg.fit(X, y)
log_reg.predict_proba(testData)
log_reg.predict(testData)

Softmax Regression

Softmax score for class $k$

$$
s_k(\boldsymbol{x})=\boldsymbol{x}^T\boldsymbol{\theta}^{(k)}
$$

Softmax function

$$
\hat{p}_k=\sigma(\boldsymbol{s}(\boldsymbol{x}))_k=\frac{exp(s_k(\boldsymbol{x}))}{\Sigma^K_{j=1}exp(s_j(\boldsymbol{x}))}
$$

  • $K$: The number of classes
  • $\boldsymbol{s}(\boldsymbol{x})$: A vector containing the scores of each class for the instance $\boldsymbol{x}$
  • $\sigma(\boldsymbol{s}(\boldsymbol{x}))_k$: The estimated probability that the instance $\boldsymbol{x}$ belongs to class $k$ given the scores of each class for that instance

Softmax regression classifier prediction

$$
\hat{y}=\underset{k}{\operatorname{arg max}}\sigma(\boldsymbol{s}(\boldsymbol{x}))_k=\underset{k}{\operatorname{arg max}}s_k(\boldsymbol{x})=\underset{k}{\operatorname{arg max}}((\boldsymbol{\theta}^{(k)})^T\boldsymbol{x})
$$

Cross entropy cost function

$$
J(\boldsymbol{\Theta})=-\frac{1}{m}\Sigma^m_{i=1}\Sigma^K_{k=1}y_k^{(i)}log(\hat{p}_k^{(i)})
$$

  • $y_k^{(i)}$: The target probability that the $i^{th}$ instance belongs to class $k$

Cross entropy gradient vector for class $k$

$$
\nabla_{\boldsymbol{\theta}^{(k)}}J(\boldsymbol{\Theta})=\frac{1}{m}\Sigma^m_{i=1}(\hat{p}_k^{(i)}-y_k^{(i)})\boldsymbol{x}^{(i)}
$$